题目内容
求证:过球O内一定点P的诸弦,被点P分成的两线段之积是一个定值.
答案:
解析:
解析:
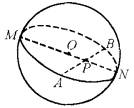
证明 设球O的半径为R,球心O到定点P的距离为d.设过P的任意一弦为AB,设过P点的直径为MN,当AB是直径MN时 MP·NP=(R+d)(R-d)=R2-d2 当AB不是直径MN时,如图所示.
MN=2R,OP=d,在MN、AB所在的大圆中,由相交弦定理知 AP·PB=MP·NP =(R+d)(R-d)=R2-d2 ∴ AP·PB为定值. 命题得证 |

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目