题目内容
“抛物线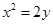 上离点
上离点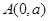 最近的点恰好为顶点”成立的充要条件是( )
最近的点恰好为顶点”成立的充要条件是( )
A.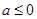 | B.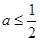 | C.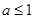 | D.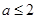 |
C
解析考点:必要条件、充分条件与充要条件的判断;抛物线的简单性质.
专题:计算题.
分析:将抛物线上的点离点A的距离用两点距离的平方表示出来,再研究二次函数的最值.
解答:解:设点P(x,y)为抛物线上的任意一点,则点P离点A(0,a)的距离的平方为
AP2=x2+(y-a)2
=x2+y2-2ay+a2
∵x2=2y
∴AP2=2y+y2-2ay+a2(y≥0)
=y2+2(1-a)y+a2(y≥0)
∴对称轴为a-1
∵离点A(0,a)最近的点恰好是顶点
∴a-1≤0解得a≤1
故选C.
点评:本题考查二次函数在给定区间的最值的求法:弄清对称轴与区间的关系,在y=0时取到最小值,故函数在定义域内递增,对称轴在区间左边.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
若椭圆的对称轴为坐标轴,长轴长为10,焦距为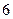 ,则椭圆的方程为
,则椭圆的方程为
A.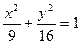 | B.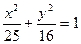 | C.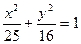 或 或 | D.以上都不对 |
设点P(x,y)(xy≠0)是曲线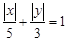 上的点,下列关系正确的是( )
上的点,下列关系正确的是( )
A. | B. |
C. | D.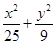 的值与1的大小关系不确定 的值与1的大小关系不确定 |
以椭圆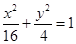 内的点
内的点 为中点的弦所在直线方程 ( )
为中点的弦所在直线方程 ( )
A.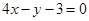 | B. | C.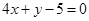 | D.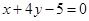 |
(文科)双曲线 的离心率是2,则k的值是( )
的离心率是2,则k的值是( )
| A.12 | B.4 | C.—12 | D.—4 |
 、
、 分别是双曲线
分别是双曲线 的左、右焦点,
的左、右焦点, 是其右顶点,过
是其右顶点,过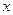 轴的垂线与双曲线的一个交点为
轴的垂线与双曲线的一个交点为 ,
, 是
是 ,则双曲线的离心率是
,则双曲线的离心率是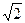
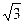
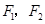 分别是椭圆
分别是椭圆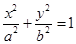 (
( )的左、右焦点,
)的左、右焦点,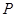 是其右准线上纵坐标为
是其右准线上纵坐标为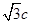 (
(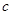 为半焦距)的点,且
为半焦距)的点,且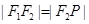 ,则椭圆的离心率是( )
,则椭圆的离心率是( )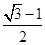
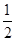
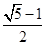
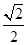
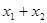 =6,那么
=6,那么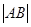 = ( *** )
= ( *** )  的顶点,过点D(0,4)的直线
的顶点,过点D(0,4)的直线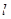 交抛物线
交抛物线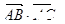 等于( )
等于( )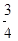 B.0 C.-3 D.
B.0 C.-3 D.