题目内容
计算(1)log2[log3(log5125)]
(2)(2a
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
分析:首先对于(1)log2[log3(log5125)]可以由里到外化简,把log1255=3代入化简即可.
对于式子(2)(2a
b
)(-6a
b
)÷(-3a
b
),看似复杂实际是有理数指数幂的简单乘法除法计算,化简即可得到答案.
对于式子(2)(2a
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
解答:解:(1)对于式子log2[log3(log5125)],需要一步一步求解,
因为:log5125=3,故原式=log2(log33)=log21=0.
故答案为0.
(2)对式子(2a
b
)(-6a
b
)÷(-3a
b
)=2×(-6)÷(-3)(a
a
÷a
)(b
b
÷b
)=4a
故答案为4a.
因为:log5125=3,故原式=log2(log33)=log21=0.
故答案为0.
(2)对式子(2a
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
故答案为4a.
点评:此题主要考查对数函数的运算和有理数指数幂的化简问题,式子看似复杂只需要一步一步化简即可得到答案,属于基础题.

练习册系列答案
相关题目
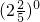 -1+log327+log2
-1+log327+log2 .
.