题目内容
已知x、y为非零实数，代数式
+
+
的值所组成的集合是M，则集合M中所有元素之和为
| |x| |
| x |
| |y| |
| y |
| |xy| |
| xy |
2
2
．分析：因为x、y为非零实数，所以解答时分四种情况进行讨论，从而求出集合M中的元素．
解答：解：因为x、y为非零实数，所以当x＞0，y＞0时，
+
+
=
+
+
=3，
当x＞0，y＜0时，
+
+
=
+
+
=-1，
当x＜0，y＞0时，
+
+
=
+
+
=-1，
当x＜0，y＜0时，
+
+
=
+
+
=-1，
所以集合M中只有两个元素-1，3，故集合M中所有元素之和为2．
故答案为2．
| |x| |
| x |
| |y| |
| y |
| |xy| |
| xy |
| x |
| x |
| y |
| y |
| xy |
| xy |
当x＞0，y＜0时，
| |x| |
| x |
| |y| |
| y |
| |xy| |
| xy |
| x |
| x |
| -y |
| y |
| -xy |
| xy |
当x＜0，y＞0时，
| |x| |
| x |
| |y| |
| y |
| |xy| |
| xy |
| -x |
| x |
| y |
| y |
| -xy |
| xy |
当x＜0，y＜0时，
| |x| |
| x |
| |y| |
| y |
| |xy| |
| xy |
| -x |
| x |
| -y |
| y |
| xy |
| xy |
所以集合M中只有两个元素-1，3，故集合M中所有元素之和为2．
故答案为2．
点评：本题考查了集合与元素关系的判断，考查了分类讨论的数学思想，解答的关键是正确把x和y分四种情况讨论．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
≥
B.(
)2≥xy
+
≥2 D.|x+y|＞|x-y|
的值所组成的集合是M，则集合M中所有元素之和为________．
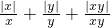的值所组成的集合是M，则集合M中所有元素之和为 ．