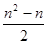题目内容
无穷数列1,3,6,10…的通项公式为( )
分析:通过观察分析可得an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+2+3+…+n,利用“累加求和”和等差数列的前n项和公式即可得出.
解答:解:∵a2-a1=3-1=2,
a3-a2=6-3=3,
a4-a3=10-6=4,
…
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+2+3+…+n=
=
.
故选C.
a3-a2=6-3=3,
a4-a3=10-6=4,
…
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+2+3+…+n=
| n(n+1) |
| 2 |
| n2+n |
| 2 |
故选C.
点评:熟练掌握“累加求和”和等差数列的前n项和公式是解题的关键.

练习册系列答案
相关题目
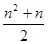 D.an=
D.an=