题目内容
若平面向量a=(1,x)和b=(2x+3,-x)互相平行,其中x∈R,
则|a-b|=( )
A. B.2或
B.2或 C.-2或0 D.2或10
C.-2或0 D.2或10
【答案】
B
【解析】
试题分析:根据题意,由于平面向量a=(1,x)和b=(2x+3,-x),可知a-b=(-2x-2,2x),而根据两个向量是互相平行的,则可知所以1×(-x)-x×(2x+3)=0?x=0,或x=-2,
则可知a=(1,0)b=(3,0),或a=(1,-2)b=(-1,2),那么求解得到a-b=(-2,0),或a-b=(2,-4),结合模的定义可知答案为2或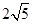 ,故选B.
,故选B.
考点:向量共线和坐标运算
点评:此题考查了两向量平行的坐标表示法及方程思想求解未知量x的值,还考查了已知向量的坐标求向量的模.

练习册系列答案
相关题目