题目内容
有一解三角形的题目,因纸张破损有一个条件丢失,具体如下:在△ABC中,已知a=
,2cos2
=(
-1)cosB,
| 3 |
| A+C |
| 2 |
| 2 |
c=
| ||||
| 2 |
c=
,求角A.经推断,破损处的条件为三角形的一边长度,且答案为A=60°.将条件补充完整填在空白处.
| ||||
| 2 |
分析:根据二倍角三角函数公式结合诱导公式化简整理,得cosB=
,所以B=45°.再分已知边b或已知边c两种情况加以讨论,结合三角形中大边对大角,可得只有已知
c=
时,A=60°,是唯一确定的解.
| ||
| 2 |
c=
| ||||
| 2 |
解答:解:∵2cos2(
)=(
-1)cosB,∴1+cos(A+C)=(
-1)cosB,即1-cosB=(
-1)cosB,整理得cosB=
.
又∵0°<B<180°,∴B=45°.
接下来分两种情况讨论:
(1)若已知边b,由
=
,求得b=
.
检验:
=
,等价于
=
,等价于sinA=
.
又因为A∈(0,π),且a>b,所以A>B,∴A=60° 或者A=120°,这与已知角A的解为唯一解矛盾.
(2)若已知边c,由B=45°,结合A=60°,得C=75°.
由
=
,可得 c=
.
检验:
=
,等价于
=
,即sinA=
.
又∵A∈(0,π),且c>a,∴只有A=60°,且此解是唯一解,符合题意.
综上所述,可得破损处应该填上:c=
,能使角A有唯一解A=60°,
故答案为 c=
.
| A+C |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
又∵0°<B<180°,∴B=45°.
接下来分两种情况讨论:
(1)若已知边b,由
| b |
| sin45° |
| ||
| sin60° |
| 2 |
检验:
| b |
| sinB |
| a |
| sinA |
| ||
| sin45° |
| ||
| sinA |
| ||
| 2 |
又因为A∈(0,π),且a>b,所以A>B,∴A=60° 或者A=120°,这与已知角A的解为唯一解矛盾.
(2)若已知边c,由B=45°,结合A=60°,得C=75°.
由
| c |
| sin75° |
| ||
| sin60° |
| ||||
| 2 |
检验:
| c |
| sinC |
| a |
| sinA |
| ||||||
| sin75° |
| ||
| sinA |
| ||
| 2 |
又∵A∈(0,π),且c>a,∴只有A=60°,且此解是唯一解,符合题意.
综上所述,可得破损处应该填上:c=
| ||||
| 2 |
故答案为 c=
| ||||
| 2 |
点评:本题给出三角形一边和一角,探索三角形有唯一解的问题,着重考查了运用正、余弦定理解三角形,和三角恒等变换等知识,属于中档题.

练习册系列答案
相关题目
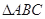 中,已知
中,已知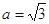 ,
, , ,求角
, ,求角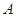 .经推断,破损处的条件为三角形的一边长度,且答案为
.经推断,破损处的条件为三角形的一边长度,且答案为 .将条件补充完整填在空白处.
.将条件补充完整填在空白处.