题目内容
已知向量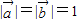 ,且
,且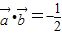 ,求:
,求:(1)
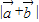 ;
;(2)
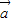 与
与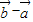 的夹角.
的夹角.
【答案】分析:(1)由已知代入模长公式计算可得;(2)同理可得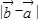 和
和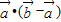 ,代入夹角公式可得夹角的余弦值,根据范围可得角.
,代入夹角公式可得夹角的余弦值,根据范围可得角.
解答:解:(1)由题意可得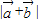 =
=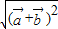
= =
= =1;
=1;
(2)同理可得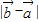 =
= =
=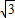
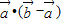 =
=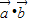 -
-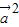 =
=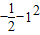 =
=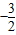 ,
,
故cos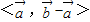 =
=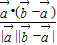 =
=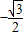 ,
,
又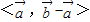 ∈[0,π],
∈[0,π],
故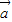 与
与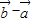 的夹角
的夹角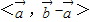 =
=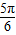
点评:本题考查平面向量的模长和夹角的求解,涉及整体代换的思想,属中档题.
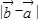 和
和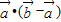 ,代入夹角公式可得夹角的余弦值,根据范围可得角.
,代入夹角公式可得夹角的余弦值,根据范围可得角.解答:解:(1)由题意可得
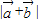 =
=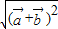
=
 =
= =1;
=1;(2)同理可得
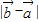 =
= =
=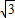
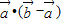 =
=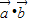 -
-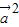 =
=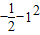 =
=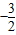 ,
,故cos
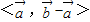 =
=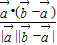 =
=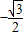 ,
,又
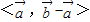 ∈[0,π],
∈[0,π],故
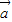 与
与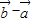 的夹角
的夹角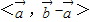 =
=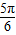
点评:本题考查平面向量的模长和夹角的求解,涉及整体代换的思想,属中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
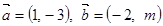 ,且
,且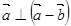 。
。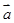 与
与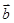 的夹角;
的夹角;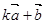 与
与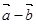 平行时,求实数
平行时,求实数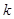 的值。
的值。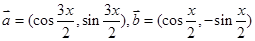 ,且
,且 。
。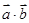 及
及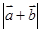 。
。