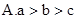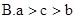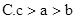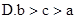题目内容
(本题满分12分)已知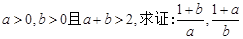 中至少有一个小于2.
中至少有一个小于2.
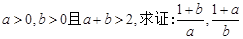 中至少有一个小于2.
中至少有一个小于2.证明见解析
涉及到至多,至少这类问题直接证明不易证的情况下可以考虑反证法.
本小题采用反证法先假设假设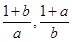 都不小于2,则
都不小于2,则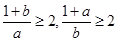 ,因为
,因为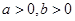 ,所以
,所以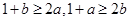 ,然后为了找到两个不等式之间的关系让两个不等式相加,从而找到证明出路.
,然后为了找到两个不等式之间的关系让两个不等式相加,从而找到证明出路.
证明:假设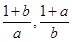 都不小于2,则
都不小于2,则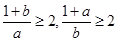 ………………2分
………………2分
因为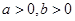 ,所以
,所以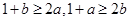 , ……………3分
, ……………3分
所以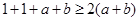 ………………3分
………………3分
即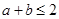 ,这与已知
,这与已知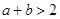 相矛盾,故假设不成立 ……………3分
相矛盾,故假设不成立 ……………3分
所以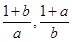 中至少有一个小于2 ……………1分
中至少有一个小于2 ……………1分
其他证法只要思路正确,推理无误,改卷老师都可以参照给分.
本小题采用反证法先假设假设
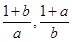 都不小于2,则
都不小于2,则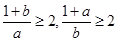 ,因为
,因为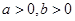 ,所以
,所以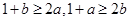 ,然后为了找到两个不等式之间的关系让两个不等式相加,从而找到证明出路.
,然后为了找到两个不等式之间的关系让两个不等式相加,从而找到证明出路.证明:假设
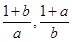 都不小于2,则
都不小于2,则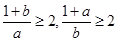 ………………2分
………………2分因为
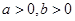 ,所以
,所以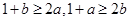 , ……………3分
, ……………3分所以
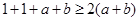 ………………3分
………………3分即
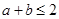 ,这与已知
,这与已知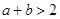 相矛盾,故假设不成立 ……………3分
相矛盾,故假设不成立 ……………3分所以
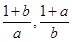 中至少有一个小于2 ……………1分
中至少有一个小于2 ……………1分其他证法只要思路正确,推理无误,改卷老师都可以参照给分.

练习册系列答案
相关题目
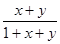 ,N=
,N=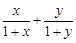 ,则M,N的大小关系是( )
,则M,N的大小关系是( )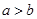 ,则
,则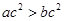
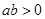 ,
,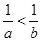
 ,则
,则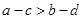
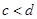 ,则
,则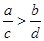
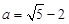 ,
,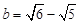 ,则
,则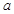 与
与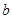 的大小关系为( )
的大小关系为( )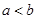
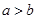
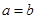
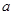
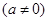 和
和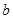 ,不等式
,不等式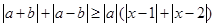 恒成立,试求实数
恒成立,试求实数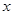 的取值范围.
的取值范围.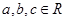 且
且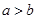 ,则下列不等式恒成立的为( )
,则下列不等式恒成立的为( )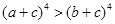
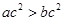
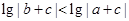
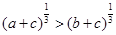
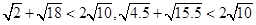 ,
,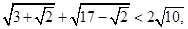 根据以上规律,试写出一个对正实数
根据以上规律,试写出一个对正实数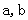 成立的条件不等式________________
成立的条件不等式________________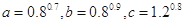 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )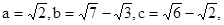 则
则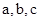 的大小顺序是( )
的大小顺序是( )