题目内容
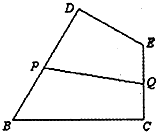 如图,某生态园欲把一块四边形地BCED辟为水果园,其中∠C=∠D=90°,BC=BD=
如图,某生态园欲把一块四边形地BCED辟为水果园,其中∠C=∠D=90°,BC=BD=| 3 |
(1)求x,y的关系式;
(2)如果PQ是灌溉水管的位置,为了省钱,希望它最短,求PQ的长的最小值;
(3)如果PQ是参观路线,希望它最长,那么P、Q的位置在哪里?
分析:(1)延长BD、CE交于A,利用S△ADE=S△BDE=S△BCE=
,S△APQ=
即可建立x,y的关系式;
(2)利用余弦定理表示出PQ,再借助于基本不等式,即可求出水管PQ的长的最小值;
(3)根据(2)中的解析式,利用换元法,将PQ2表示成PQ2=f(t)=t+
-12,利用导数,确定函数的单调性,从而得到函数的最大值.
| ||
| 2 |
| 3 |
(2)利用余弦定理表示出PQ,再借助于基本不等式,即可求出水管PQ的长的最小值;
(3)根据(2)中的解析式,利用换元法,将PQ2表示成PQ2=f(t)=t+
| 48 |
| t |
解答: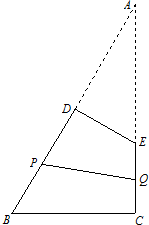 解:(1)延长BD、CE交于点A,
解:(1)延长BD、CE交于点A,
设AD=a,在Rt△ABC中,BC=
,AB=
+a,则AC=
=
,
∵△ADE∽△ACB,且DE=1,
∴
=
,即
=
,
解得a=
,即AD=
,
在Rt△ADE中,AE=
=
=2,
∴S△ADE=
×AD×DE=
,S△BDE=
×BD×DE=
,S△BCE=
×BC×CE=
,
∵SBCED=S△BDE+S△BCE=2×
=
,
∵PQ将四边形BCED分成面积相等的两部分,
∴S△APQ=
SBCED+S△ADE=
,
∴
(x+
)(y+2)=
,
∴(x+
)(y+2)=4
,
∴x,y的关系式为(x+
)(y+2)=4
;
(2)在△APQ中,由余弦定理可得,PQ2=AP2+AQ2-2AP•AQcos30°=(x+
)2+(
)2-2×4
×
≥2
-2×4
×
=8
-12,
当且仅当(x+
)2=(
)2,即x=2
-
时取等号,
∴PQmin=
=2
,
∴PQ的长的最小值为2
;
(3)由(2)可知,PQ2=(x+
)2+(
)2-2×4
×
,
令t=(x+
)2,
∵x∈[
,
],
∴t∈[
,12],
∴PQ2=f(t)=t+
-12,
∵f′(t)=1-
,令f′(t)=1-
=0,解得t=4
,
∵当t∈(0,4
)时,f′(t)<0,则f(t)在(0,4
)上是减函数,
当t∈(4
,+∞)时,f′(t)>0,则f(t)在(4
,+∞)上是增函数,
∴f(t)max=max{f(
),f(12)}=f(12)=4,
∴PQmax=2,
∵t=(x+
)2=12,
∴x=
,
∵(x+
)(y+2)=4
,
∴y=0,
∴P点在B处,Q点在E处.
 解:(1)延长BD、CE交于点A,
解:(1)延长BD、CE交于点A,设AD=a,在Rt△ABC中,BC=
| 3 |
| 3 |
(
|
2
|
∵△ADE∽△ACB,且DE=1,
∴
| AD |
| AC |
| DE |
| BC |
| a | ||||
|
| 1 | ||
|
解得a=
| 3 |
| 3 |
在Rt△ADE中,AE=
| AD2+DE2 |
|
∴S△ADE=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∵SBCED=S△BDE+S△BCE=2×
| ||
| 2 |
| 3 |
∵PQ将四边形BCED分成面积相等的两部分,
∴S△APQ=
| 1 |
| 2 |
| 3 |
∴
| 1 |
| 4 |
| 3 |
| 3 |
∴(x+
| 3 |
| 3 |
∴x,y的关系式为(x+
| 3 |
| 3 |
(2)在△APQ中,由余弦定理可得,PQ2=AP2+AQ2-2AP•AQcos30°=(x+
| 3 |
4
| ||
x+
|
| 3 |
| ||
| 2 |
(x+
|
| 3 |
| ||
| 2 |
| 3 |
当且仅当(x+
| 3 |
4
| ||
x+
|
| 4 | 3 |
| 3 |
∴PQmin=
8
|
2
|
∴PQ的长的最小值为2
2
|
(3)由(2)可知,PQ2=(x+
| 3 |
4
| ||
x+
|
| 3 |
| ||
| 2 |
令t=(x+
| 3 |
∵x∈[
| ||
| 3 |
| 3 |
∴t∈[
| 16 |
| 3 |
∴PQ2=f(t)=t+
| 48 |
| t |
∵f′(t)=1-
| 48 |
| t2 |
| 48 |
| t2 |
| 3 |
∵当t∈(0,4
| 3 |
| 3 |
当t∈(4
| 3 |
| 3 |
∴f(t)max=max{f(
| 16 |
| 3 |
∴PQmax=2,
∵t=(x+
| 3 |
∴x=
| 3 |
∵(x+
| 3 |
| 3 |
∴y=0,
∴P点在B处,Q点在E处.
点评:本题主要考查函数模型的选择与应用,利用导数研究函数的单调性,利用导数求函数在闭区间上的最值,余弦定理的应用.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.本题中的数学模型求最值,应用了基本不等式求最值和导数求最值.属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 辟为水果园,其中
辟为水果园,其中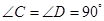 ,
,
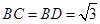 ,
,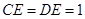 .若经过
.若经过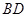 上一点
上一点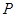 和
和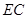 上一点
上一点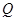 铺设一条道路
铺设一条道路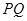 ,且
,且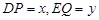 .
.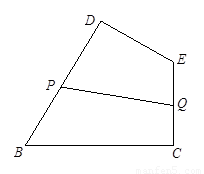
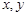 的关系式;
的关系式;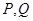 的位置在哪里?
的位置在哪里?