题目内容
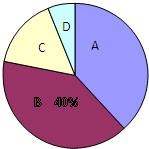2013年4月9日至14日，西安市共有35000余名学生参加中考体育测试，为了了解九年级男生立定跳远的成绩，从某校随机抽取了50名男生的测试成绩，根据测试评分标准，将他们的得分按优秀、良好、及格、不及格（分别用A、B、C、D表示）四个等级进行统计，并绘制成下面的扇形图和统计表：| 等级 | 成绩（分） | 频数（人数） | 频率 |
| A | 90～100 | 19 | 0.38 |
| B | 75～89 | m | x |
| C | 60～74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
（1）m=
20
20
，n═8
8
，x=0.4
0.4
，y=0.16
0.16
；（2）在扇形图中，B等级所对应的圆心角是
144
144
度；（3）如果该校九年级共有500名男生参加了立定跳远测试，那么请你估计这些男生成绩等级达到优秀和良好的共有多少人？
分析：（1）根据成绩为B等级的学生占得比例为40%，可得频数m和频率x的值，再根据各个等级的频数之和等于50，求得n；再根据各个等级的频率之和等于1，
求得y=0.16，从而得到答案．
（2）在扇形图中，B等级所对应的圆心角的度数等于360°乘以B等级所占的比例．
（3）由频率分步表可得成绩等级达到优秀和良好的频率之和为 0.38+0.4=0.78，再将此值乘以500，即得所求．
求得y=0.16，从而得到答案．
（2）在扇形图中，B等级所对应的圆心角的度数等于360°乘以B等级所占的比例．
（3）由频率分步表可得成绩等级达到优秀和良好的频率之和为 0.38+0.4=0.78，再将此值乘以500，即得所求．
解答：解：（1）根据成绩为B等级的学生占得比例为40%，可得频数 m=50×40%=20，频率x=0.4．
再根据各个等级的频数之和等于50，求得n=8；再根据各个等级的频率之和等于1，求得y=0.16．
故答案为 20、8、0.4、0.16．
（2）在扇形图中，B等级所对应的圆心角是360°×40%=144°，
故答案为 144．
（3）由频率分步表可得成绩等级达到优秀和良好的频率之和为 0.38+0.4=0.78，
故成绩等级达到优秀和良好的人数为500×0.78=390．
再根据各个等级的频数之和等于50，求得n=8；再根据各个等级的频率之和等于1，求得y=0.16．
故答案为 20、8、0.4、0.16．
（2）在扇形图中，B等级所对应的圆心角是360°×40%=144°，
故答案为 144．
（3）由频率分步表可得成绩等级达到优秀和良好的频率之和为 0.38+0.4=0.78，
故成绩等级达到优秀和良好的人数为500×0.78=390．
点评：本题主要考查频率分步表的性质，用样本频率估计总体分布，属于基础题．
练习册系列答案
相关题目
