题目内容
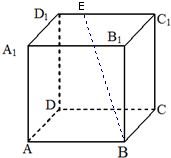 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E是D1C1上的一点且EC1=3D1 E,
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E是D1C1上的一点且EC1=3D1 E,(1)求直线BE与平面ABCD所成角的大小;
(2)求异面直线BE与CD所成角的大小.(以上结果均用反三角函数表示)
分析:(1)在DC上取一点F,使DF=1,连接EF,则EF⊥平面ABCD,再连接FB,则∠EBF为直线BE与平面ABCD所成角,故可求;
(2)由于AB∥CD,可知∠EBA(或其补角)是异面直线BE与DC所成的角.连接AD1与AE,在Rt△AD1E中,可求异而直线BE与CD所成角的大小.
(2)由于AB∥CD,可知∠EBA(或其补角)是异面直线BE与DC所成的角.连接AD1与AE,在Rt△AD1E中,可求异而直线BE与CD所成角的大小.
解答: 解:(1)在DC上取一点F,使DF=1,连接EF,则EF⊥平面ABCD,
解:(1)在DC上取一点F,使DF=1,连接EF,则EF⊥平面ABCD,
再连接FB,则∠EBF为直线BE与平面ABCD所成角,…(3分)
∵BF=5,∴tan∠EBF=
,故直线BE与平面ABCD所成角为arctan
…(6分)
(2)由题意AB∥CD,∴∠EBA(或其补角)是异面直线BE与DC所成的角.…(8分)
连接AD1与AE,在Rt△AD1E中,可得AE=
,
又在Rt△BEC1中,可得BE=
∴cos∠EBA=
…(10分)
∴异而直线BE与CD所成角的大小为arccos
…(12分)
 解:(1)在DC上取一点F,使DF=1,连接EF,则EF⊥平面ABCD,
解:(1)在DC上取一点F,使DF=1,连接EF,则EF⊥平面ABCD,再连接FB,则∠EBF为直线BE与平面ABCD所成角,…(3分)
∵BF=5,∴tan∠EBF=
| 4 |
| 5 |
| 4 |
| 5 |
(2)由题意AB∥CD,∴∠EBA(或其补角)是异面直线BE与DC所成的角.…(8分)
连接AD1与AE,在Rt△AD1E中,可得AE=
| 33 |
又在Rt△BEC1中,可得BE=
| 41 |
∴cos∠EBA=
3
| ||
| 41 |
∴异而直线BE与CD所成角的大小为arccos
3
| ||
| 41 |
点评:本题以正方体为载体,考查线面角,考查线线角,关键是正确作出相应的角.

练习册系列答案
相关题目
 (2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )
(2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )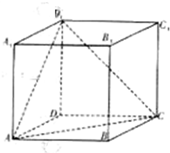 如图,正方体ABCD-A1B1C1D1的棱长为4,点P从B点出发,在正方形BCC1B1的边上按逆针方向按如下规律运动:设第n次运动的路程为an,且
如图,正方体ABCD-A1B1C1D1的棱长为4,点P从B点出发,在正方形BCC1B1的边上按逆针方向按如下规律运动:设第n次运动的路程为an,且 如图,在正三棱柱ABC-A1B1C1中,点D,D1分别为棱BC,B1C1的中点.
如图,在正三棱柱ABC-A1B1C1中,点D,D1分别为棱BC,B1C1的中点.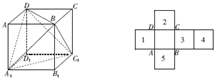 (2011•安徽模拟)下面关于棱长为1的正方体ABCD-A1B1C1D1叙述正确的是
(2011•安徽模拟)下面关于棱长为1的正方体ABCD-A1B1C1D1叙述正确的是 平面
平面 ,垂足为
,垂足为 ,正四面体
,正四面体 的棱长为4,
的棱长为4, 在平面
在平面 是直线
是直线 上的动点,则当
上的动点,则当 的距离为最大时,正四面体在平面
的距离为最大时,正四面体在平面 B.
B. C.
C. D.
D.
