题目内容
在下列命题中:①方程|x|+|y|=1表示的曲线所围成区域为面积为2;
②与两个坐标轴距离相等的点的轨迹方程为y=±x;
③与两定点(-1,0),(1,0)距离之和等于1的点的轨迹为椭圆;
④与两定点(-1,0),(1,0)距离之差的绝对值等于1的点的轨迹为双曲线.
正确的命题的序号是 .(注:把你认为正确的命题序号都填上)
【答案】分析:①:方程|x|+|y|=1表示的曲线所围成区域为边长为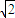 的正方形②:与两个坐标轴距离相等的点的轨迹方程为|x|=|y|即y=±x,③:由于两定点(-1,0),(1,0)距离为2>1,根据椭圆的定义可知此时的点的轨迹不存在④:根据双曲线的定义进行判断
的正方形②:与两个坐标轴距离相等的点的轨迹方程为|x|=|y|即y=±x,③:由于两定点(-1,0),(1,0)距离为2>1,根据椭圆的定义可知此时的点的轨迹不存在④:根据双曲线的定义进行判断
解答:解:①:方程|x|+|y|=1表示的曲线所围成区域为边长为 的正方形,故面积为2,故①正确
的正方形,故面积为2,故①正确
②:与两个坐标轴距离相等的点的轨迹方程为|x|=|y|即y=±x,故②正确
③:由于两定点(-1,0),(1,0)距离为2>1,根据椭圆的定义可知此时的点的轨迹不存在,③错误
④:根据双曲线的定义可知④正确
故答案为:①②④
点评:本题主要考查了线性规划的知识,点的轨迹方程的应用,椭圆与双曲线的定义的应用,尤其是③④中一定要注意椭圆与双曲线成立的条件.
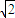 的正方形②:与两个坐标轴距离相等的点的轨迹方程为|x|=|y|即y=±x,③:由于两定点(-1,0),(1,0)距离为2>1,根据椭圆的定义可知此时的点的轨迹不存在④:根据双曲线的定义进行判断
的正方形②:与两个坐标轴距离相等的点的轨迹方程为|x|=|y|即y=±x,③:由于两定点(-1,0),(1,0)距离为2>1,根据椭圆的定义可知此时的点的轨迹不存在④:根据双曲线的定义进行判断解答:解:①:方程|x|+|y|=1表示的曲线所围成区域为边长为
 的正方形,故面积为2,故①正确
的正方形,故面积为2,故①正确②:与两个坐标轴距离相等的点的轨迹方程为|x|=|y|即y=±x,故②正确
③:由于两定点(-1,0),(1,0)距离为2>1,根据椭圆的定义可知此时的点的轨迹不存在,③错误
④:根据双曲线的定义可知④正确
故答案为:①②④
点评:本题主要考查了线性规划的知识,点的轨迹方程的应用,椭圆与双曲线的定义的应用,尤其是③④中一定要注意椭圆与双曲线成立的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目