题目内容
若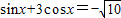
，则tanx=（ ）A．
B．3
C．
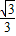
D．
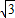
【答案】分析：由已知的等式表示出sinx，代入sin2x+cos2x=1，得到关于cosx的方程，求出方程的解得到cosx的值，进而确定出sinx的值，利用同角三角函数间的基本关系即可得到tanx的值．
解答：解：由sinx+3cosx=-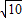
，得到sinx=-
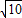-3cosx，
代入sin2x+cos2x=1中得：10+6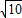
cosx+10cos2x-1=0，
即（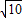
cosx+3）2=0，解得：cosx=-
，
∴sinx=-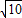
-3×（-
）=-
，
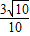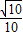则tanx=
．
故选A
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
解答：解：由sinx+3cosx=-
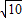，得到sinx=-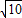-3cosx，代入sin2x+cos2x=1中得：10+6
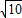cosx+10cos2x-1=0，即（
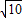cosx+3）2=0，解得：cosx=-，∴sinx=-
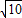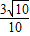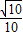-3×（-）=-，则tanx=
．故选A
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
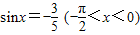，则tanx= ．
；
，则tanx+cotx的值为2；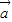
=（1，sin2x），
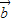=（2，sin2x），其中x∈（0，π），若|
|=|
|•|
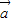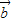|，则tanx的值等于 ．
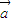=（1，sin2x），
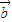=（2，sin2x），其中x∈（0，π），若|
|=|
|•|
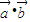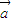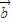|，则tanx的值等于 ．