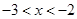题目内容
已知不等式![]()
![]() 的解集是
的解集是![]()
(1)求实数![]() 的取值范围:
的取值范围:
(2)在(1)的条件下,当实数![]() 取得最大值时,试判断
取得最大值时,试判断![]() 是否成立?并证明你的结论。
是否成立?并证明你的结论。
解:(1)由绝对值不等式性质知:
![]() 对
对![]() 恒成立
恒成立
故![]() 的解集为
的解集为![]() ,只须
,只须![]() 既可
既可
![]()
![]() 的取值范围是
的取值范围是![]()
由(1)知实数![]() 的最大值为3
的最大值为3
当![]() 时,不等式
时,不等式![]() 成立
成立
证明如下:利用分析法
要使![]() 成立
成立
只须![]()
等价于 ![]()
等价于 ![]()
等价于 ![]() ,而
,而![]() 显然成立,以上每一步均可逆推,故所证明不等式成立。
显然成立,以上每一步均可逆推,故所证明不等式成立。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
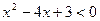 的解集是
的解集是 .
.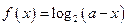
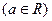 的定义域为集合
的定义域为集合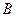 ,若
,若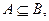
 求
求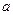 的取值范围;
的取值范围;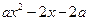

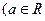 且
且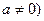 的解集为
的解集为 ,若
,若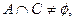 求
求 值范围.
值范围.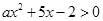 的解集是
的解集是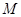 .
.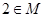 ,求
,求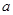 的取值范围;
的取值范围; ,求不等式
,求不等式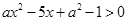 的解集.
的解集. 的解集是
的解集是 ,则
,则  B、
B、
 D、
D、
 的解集是
的解集是 ,则不等式
,则不等式 的解是( )
的解是( )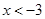 或
或 B、
B、 或
或
 D、
D、
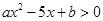 的解集是
的解集是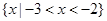 ,则不等式
,则不等式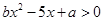 的
的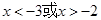 B.
B.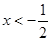 或
或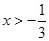 C.
C.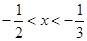 D.
D.