题目内容
设不等式组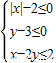 所表示的平面区域为S,若A,B为S内的两个点,则|AB|的最大值为 .
所表示的平面区域为S,若A,B为S内的两个点,则|AB|的最大值为 .
【答案】分析:先由线性约束条件画出区域,欲求|AB|的最大值,观察平面区域知,D、F两点距离最大,故只要求出此两点的距离即得.
解答: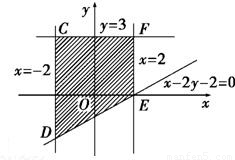 解:原不等式组可以化为
解:原不等式组可以化为 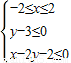 ,
,
画出对应的平面区域图形如图所示的阴影部分.
坐标依次为F(2,3),D(-2,-2).
显然在平面区域内,D、F两点距离最大为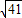 ,
,
即|AB|的最大值为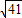 .
.
故答案为: .
.
点评:本题只是直接考查线性规划问题,是一道较为简单的送分题.线性规划问题高考数学考试的热点,数形结合是数学思想的重要手段之一,是连接代数和几何的重要方法.线性规划这一类新型数学应用问题要引起重视.
解答:
 解:原不等式组可以化为
解:原不等式组可以化为 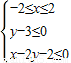 ,
,画出对应的平面区域图形如图所示的阴影部分.
坐标依次为F(2,3),D(-2,-2).
显然在平面区域内,D、F两点距离最大为
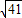 ,
,即|AB|的最大值为
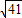 .
.故答案为:
 .
.点评:本题只是直接考查线性规划问题,是一道较为简单的送分题.线性规划问题高考数学考试的热点,数形结合是数学思想的重要手段之一,是连接代数和几何的重要方法.线性规划这一类新型数学应用问题要引起重视.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 所表示的平面区域内的概率.
所表示的平面区域内的概率.