题目内容
【题目】在平面直角坐标系中,![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,动点
,动点![]() 满足:直线
满足:直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 作两条互相垂直的射线,与(1)的轨迹分别交于
作两条互相垂直的射线,与(1)的轨迹分别交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)由题意得,利用![]() ,即
,即![]() ,即可求解椭圆的标准方程;(2)设
,即可求解椭圆的标准方程;(2)设![]() ,
,![]() ,把直线方程与椭圆的方程联立,可得根与系数的关系、弦长关系、点到直线的距离公式,即可求解出三角形的面积表示,在利用基本不等式即可求解面积的最小值.
,把直线方程与椭圆的方程联立,可得根与系数的关系、弦长关系、点到直线的距离公式,即可求解出三角形的面积表示,在利用基本不等式即可求解面积的最小值.
试题解析:(1)已知![]() ,
,![]() ,设动点
,设动点![]() 的坐标
的坐标![]() ,
,
所以直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]()
![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() .
.
(2)设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,与椭圆
,与椭圆![]() 联立
联立
消去![]() 得
得![]() ,
,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
即![]() ,把
,把![]() ,
,![]()
代入得![]() ,
,
整理得![]() ,所以
,所以![]() 到直线
到直线![]() 的距离
的距离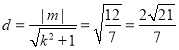 .
.
∵![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时取“=”号.
时取“=”号.
由![]() 得
得![]() ,∴
,∴![]() ,
,
即弦![]() 的长度的最小值是
的长度的最小值是![]() .
.
所以三角形的最小面积为![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
【题目】某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此判断哪组工人的技术水平更好;
(2)质监部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,否则“不合格”.求该车间“质量不合格”的概率.
