题目内容
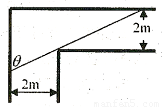
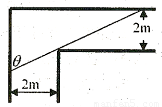
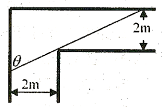 一铁棒欲水平通过如图所示的直角走廊,试回答下列问题:
一铁棒欲水平通过如图所示的直角走廊,试回答下列问题:(1)用θ表示铁棒的长度L(θ);
(2)若铁棒能通过该直角走廊,求铁棒长度的最大值.
分析:(1)利用直角三角形中的函数,即可用θ表示铁棒的长度L(θ);
(2)解法一,利用换元法,确定函数单调递减;解法二:利用导数,确定函数的单调性,即可得到结论.
(2)解法一,利用换元法,确定函数单调递减;解法二:利用导数,确定函数的单调性,即可得到结论.
解答:解:(1)根据题中图形可知,L(θ)=
+
,θ∈(0,
).…(4分)
(2)本题即求L(θ)的最小值.…(5分)
解法一:L(θ)=
+
=2
,
令t=sinθ+cosθ,t∈(1,
],原式可化为L(t)=
=
…(9分)
因为L(t)为减函数,所以L(t)≥L(
)=4
.…(11分)
所以铁棒的最大长度为4
m.…(12分)
解法二:因为
,所以
=
…(9分)
因为θ∈(0,
),所以θ∈(0,
]时,L(θ)为减函数,θ∈[
,
)时,L(θ)为增函数,所以L(θ)min=L(
)=4
,…(12分)
| 2 |
| cosθ |
| 2 |
| sinθ |
| π |
| 2 |
(2)本题即求L(θ)的最小值.…(5分)
解法一:L(θ)=
| 2 |
| cosθ |
| 2 |
| sinθ |
| sinθ+cosθ |
| sinθ•cosθ |
令t=sinθ+cosθ,t∈(1,
| 2 |
| 4t |
| t2-1 |
| 4 | ||
t-
|
因为L(t)为减函数,所以L(t)≥L(
| 2 |
| 2 |
所以铁棒的最大长度为4
| 2 |
解法二:因为
|
|
=
| 2(sinθ-cosθ)(sin2θ+sinθcosθ+cos2θ) |
| sin2θcos2θ |
因为θ∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 2 |
点评:本题考查函数模型的构建,考查导数知识的运用,确定函数的单调性是关键.

练习册系列答案
相关题目