题目内容
课本中介绍了诺贝尔奖,其发放方式为:每年一次,把奖金总金额平均分成6份,奖励在6项(物理、化学、文学、经济学、生理学和医学、和平)为人类作出了最有益贡献的人.每年发放奖金的总金额是基金在该年度所获利息的一半,另一半利息用于增加基金总额,以便保证奖金数逐年递增.资料显示:1998年诺贝尔奖发奖后基金总额已达19516万美元,假设基金平均年利率为
r=6.24%.
(1)请计算:1999年诺贝尔奖发奖后基金总额为多少万美元?当年每项奖金发放多少万美元(结果精确到1万美元)?
(2)设f(x)表示为第x(x∈N*)年诺贝尔奖发奖后的基金总额(1998年记为f(1)),试求函数f(x)的表达式.并据此判断新民网一则新闻“2008年度诺贝尔奖各项奖金高达168万美元”是否与计算结果相符,并说明理由.
解:(1)由题意知:1999年诺贝尔奖发奖后基金总额为
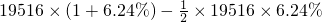 =20124.8992≈20125万美元;
=20124.8992≈20125万美元;
每项奖金发放额为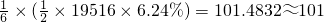 万美元;
万美元;
(2)由题意知:f(1)=19516,
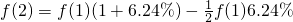 =f(1)•(1+3.12%),
=f(1)•(1+3.12%),
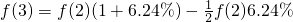 =f(2)•(1+3.12%)=f(1)•(1+3.12%)2
=f(2)•(1+3.12%)=f(1)•(1+3.12%)2
所以,f(x)=19516•(1+3.12%)x-1(x∈N*).
2007年诺贝尔奖发奖后基金总额为f(10)=19516•(1+3.12%)9
2008年度诺贝尔奖各项奖金额为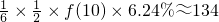 万美元,
万美元,
与168万美元相比少了34万美元,计算结果与新闻不符.
分析:(1)由题意先求得1999年诺贝尔奖发奖后基金总额和每项奖金发放额即可;
(2)由题意先求得f(1),f(2)和f(3),结合指数式的特点,由此归纳出f(x)的表达式,再计算出2007年诺贝尔奖发放后基金总额及2008的度诺贝尔奖各项金额发现与168万美元相比少了约34万美元,从而判断出新闻的真实性.
点评:本小题主要考查函数模型的选择与应用、函数值、归纳推理等,属于基础题.解决实际问题的关键是建立数学模型.
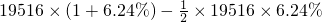 =20124.8992≈20125万美元;
=20124.8992≈20125万美元; 每项奖金发放额为
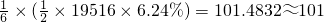 万美元;
万美元; (2)由题意知:f(1)=19516,
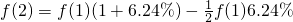 =f(1)•(1+3.12%),
=f(1)•(1+3.12%),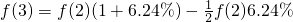 =f(2)•(1+3.12%)=f(1)•(1+3.12%)2
=f(2)•(1+3.12%)=f(1)•(1+3.12%)2所以,f(x)=19516•(1+3.12%)x-1(x∈N*).
2007年诺贝尔奖发奖后基金总额为f(10)=19516•(1+3.12%)9
2008年度诺贝尔奖各项奖金额为
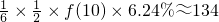 万美元,
万美元,与168万美元相比少了34万美元,计算结果与新闻不符.
分析:(1)由题意先求得1999年诺贝尔奖发奖后基金总额和每项奖金发放额即可;
(2)由题意先求得f(1),f(2)和f(3),结合指数式的特点,由此归纳出f(x)的表达式,再计算出2007年诺贝尔奖发放后基金总额及2008的度诺贝尔奖各项金额发现与168万美元相比少了约34万美元,从而判断出新闻的真实性.
点评:本小题主要考查函数模型的选择与应用、函数值、归纳推理等,属于基础题.解决实际问题的关键是建立数学模型.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目