题目内容
已知数列![]() 满足:
满足:![]() 且对任意的
且对任意的![]() 有
有![]() .
.
(Ⅰ)求数列![]() 的通项公式
的通项公式![]() ;
;
(Ⅱ)是否存在等差数列![]() ,使得对任意的
,使得对任意的![]() 有
有![]() 成立?证明你的结论
成立?证明你的结论
(Ⅰ) ![]()
(Ⅱ)![]() ,即
,即![]()
解析:
(Ⅰ)解:∵![]()
∴![]()
![]()
∴数列![]() 是首项为(
是首项为(![]() ),公比为2的等比数列,………………4分
),公比为2的等比数列,………………4分
![]() ,
,![]()
![]()
![]()
![]() ,∴数列
,∴数列![]() 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列
![]() ,∴
,∴![]() … …………………7分
… …………………7分
(Ⅱ)令![]() 代入
代入![]() 得:
得:
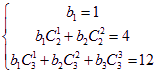 解得:
解得:![]()
由此可猜想![]() ,即
,即![]() …………………10分
…………………10分
下面用数学归纳法证明:
(1)当n=1时,等式左边=1,右边=![]() ,
,
![]() 当n=1时,等式成立,
当n=1时,等式成立,
(2)假设当n=k时,等式成立,即![]()
当n=k+1时
![]()
![]()
![]()
![]()
![]()
∴当n=k+1时,等式成立,
综上所述,存在等差数列![]() ,使得对任意的
,使得对任意的![]() 有
有![]() 成立。 …………………14分
成立。 …………………14分

练习册系列答案
相关题目
 满足
满足 ,且对任意的
,且对任意的 都有
都有

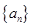 满足
满足 ,且对任意的正整数
,且对任意的正整数 都有
都有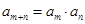 ,若数列
,若数列 项和为
项和为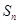 ,则
,则