题目内容
已知凸函数的性质定理:如果函数f(x)在区间D上是凸函数,则对于区间内的任意x1,x2,…,xn,有 [f(x1)+f(x2)+…+f(xn)]≤
[f(x1)+f(x2)+…+f(xn)]≤ .已知y=sinx在区间(0,π)上是凸函数,那么在△ABC中,sinA+sinB+sinC的最大值为( )
.已知y=sinx在区间(0,π)上是凸函数,那么在△ABC中,sinA+sinB+sinC的最大值为( )A.

B.

C.

D.

【答案】分析:据题意得 (sinA+sinB+sinC)≤
(sinA+sinB+sinC)≤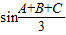 ,结合A,B,C为△ABC的三个内角,和为π,可得答案.
,结合A,B,C为△ABC的三个内角,和为π,可得答案.
解答:解:据题意得 (sinA+sinB+sinC)≤
(sinA+sinB+sinC)≤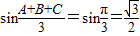 .
.
∴sinA+sinB+sinC≤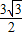 .
.
故选B
点评:本题考查的知识点是三角函数的最值,其中根据已知中凸函数的定义,得到 (sinA+sinB+sinC)≤
(sinA+sinB+sinC)≤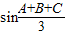 是解答本题的关键.
是解答本题的关键.
 (sinA+sinB+sinC)≤
(sinA+sinB+sinC)≤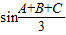 ,结合A,B,C为△ABC的三个内角,和为π,可得答案.
,结合A,B,C为△ABC的三个内角,和为π,可得答案.解答:解:据题意得
 (sinA+sinB+sinC)≤
(sinA+sinB+sinC)≤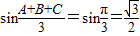 .
.∴sinA+sinB+sinC≤
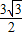 .
.故选B
点评:本题考查的知识点是三角函数的最值,其中根据已知中凸函数的定义,得到
 (sinA+sinB+sinC)≤
(sinA+sinB+sinC)≤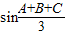 是解答本题的关键.
是解答本题的关键. 
练习册系列答案
相关题目
 在区间
在区间 上是凸函数,则对于区间
上是凸函数,则对于区间 ,有:
,有: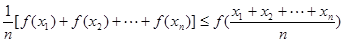 ”.若函数
”.若函数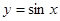 在区间
在区间 上是凸函数,则在
上是凸函数,则在 中,
中, 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.