题目内容
已知点列B1(1,b1),B2(2,b2),…,Bn(n,bn),…(n∈N)顺次为抛物线y= x2
x2
上的点,过点Bn(n,bn)作抛物线y= x2的切线交x轴于点An(an,0),点Cn(cn,0)在x轴上,且点An,Bn,Cn构成以点Bn为顶点的等腰三角形.
x2的切线交x轴于点An(an,0),点Cn(cn,0)在x轴上,且点An,Bn,Cn构成以点Bn为顶点的等腰三角形.
(1)求数列{an},{cn}的通项公式;
(2)是否存在n使等腰三角形AnBnCn为直角三角形,
若有,请求出n;若没有,请说明理由.
(3)设数列{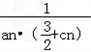 }的前n项和为Sn,求证:
}的前n项和为Sn,求证: ≤Sn<
≤Sn< .
.
 x2
x2上的点,过点Bn(n,bn)作抛物线y=
 x2的切线交x轴于点An(an,0),点Cn(cn,0)在x轴上,且点An,Bn,Cn构成以点Bn为顶点的等腰三角形.
x2的切线交x轴于点An(an,0),点Cn(cn,0)在x轴上,且点An,Bn,Cn构成以点Bn为顶点的等腰三角形.(1)求数列{an},{cn}的通项公式;
(2)是否存在n使等腰三角形AnBnCn为直角三角形,
若有,请求出n;若没有,请说明理由.
(3)设数列{
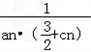 }的前n项和为Sn,求证:
}的前n项和为Sn,求证: ≤Sn<
≤Sn< .
.解:∵y= x2,∴y′=
x2,∴y′= ,y′|x=n=
,y′|x=n= ,
,
∴点Bn(n,bn)作抛物线y= x2的切线方程为:y﹣
x2的切线方程为:y﹣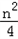 =
= (x﹣n),
(x﹣n),
令y=0,则x= ,即an=
,即an= ;
;
∵点An,Bn,Cn构成以点Bn为顶点的等腰三角形,
∴an+cn=2n,∴cn=2n﹣an=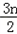
(2)解:若等腰三角形AnBnCn为直角三角形,
则|AnCn|=2bn∴n=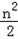 ,∴n=2,
,∴n=2,
∴存在n=2,使等腰三角形A2B2C2为直角三角形
(3)证明:∵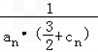 =
=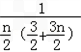 =
=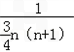 =
= (
( ﹣
﹣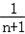 )
)
Sn= (1﹣
(1﹣ +
+ ﹣
﹣ +…+
+…+ ﹣
﹣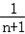 )=
)= (1﹣
(1﹣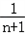 )<
)<
又1﹣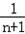 随n的增大而增大,
随n的增大而增大,
∴当n=1时,Sn的最小值为: (1﹣
(1﹣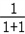 )=
)= ,
,
∴ ≤Sn<
≤Sn<
 x2,∴y′=
x2,∴y′= ,y′|x=n=
,y′|x=n= ,
,∴点Bn(n,bn)作抛物线y=
 x2的切线方程为:y﹣
x2的切线方程为:y﹣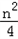 =
= (x﹣n),
(x﹣n),令y=0,则x=
 ,即an=
,即an= ;
;∵点An,Bn,Cn构成以点Bn为顶点的等腰三角形,
∴an+cn=2n,∴cn=2n﹣an=
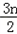
(2)解:若等腰三角形AnBnCn为直角三角形,
则|AnCn|=2bn∴n=
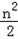 ,∴n=2,
,∴n=2,∴存在n=2,使等腰三角形A2B2C2为直角三角形
(3)证明:∵
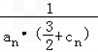 =
=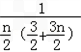 =
=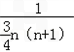 =
= (
( ﹣
﹣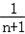 )
)Sn=
 (1﹣
(1﹣ +
+ ﹣
﹣ +…+
+…+ ﹣
﹣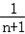 )=
)= (1﹣
(1﹣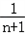 )<
)<
又1﹣
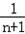 随n的增大而增大,
随n的增大而增大,∴当n=1时,Sn的最小值为:
 (1﹣
(1﹣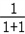 )=
)= ,
,∴
 ≤Sn<
≤Sn<

练习册系列答案
相关题目
 的坐标为
的坐标为 )1005-1])
)1005-1]) )1005-1])
)1005-1]) )2010-1])
)2010-1]) )2010-1])
)2010-1]) B.
B.
 D.
D.