题目内容
已知:如图,矩形 ,
, 平面
平面 ,
, 分别是
分别是 的中点,
的中点,
(1)求证:直线 直线
直线 ,
,
(2)若平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为 ,能否确定
,能否确定 使直线
使直线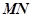 是异面直线
是异面直线 与
与 的公垂线.若能确定,求出
的公垂线.若能确定,求出 的值;若不能确定,说明理由。
的值;若不能确定,说明理由。

【答案】
 时,
时, 为
为 ,
, 的公垂线
的公垂线
【解析】(1)证明:取 中点
中点 ,连结
,连结 ,
,
则

 ,
,

 ,
,



 ,
,
 四边形
四边形 为平行四边形,
为平行四边形,

 //
// 。
。


 平面
平面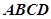 ,
,
 平面
平面
 平面
平面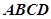 ,
,



 ,
,

 平面
平面 ,
,



 ,
,



(2) 
 //
// ,
,


 平面
平面 ,
,
 为二面角
为二面角 的平面角,
的平面角,


 ,
,
若 为
为 ,
, 的公垂线,
的公垂线,
则

 ,又
,又
 平面
平面 ,
,



 ,
,

 平面
平面 ,
,



 ,
,
 为
为 中点,
中点,
 ,
,
于是可以确定 时,
时, 为
为 ,
, 的公垂线。
的公垂线。
高&考%资(源

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
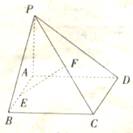 (13分)如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。
(13分)如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。 (13分)如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。
(13分)如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。