题目内容
(本题满分13分)设函数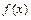 是定义在
是定义在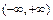 上的增函数,是否存在这样的实数
上的增函数,是否存在这样的实数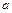 ,使得不等式
,使得不等式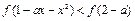 对于任意
对于任意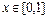 都成立?若存在,试求出实数
都成立?若存在,试求出实数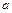 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
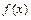 是定义在
是定义在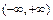 上的增函数,是否存在这样的实数
上的增函数,是否存在这样的实数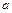 ,使得不等式
,使得不等式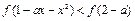 对于任意
对于任意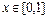 都成立?若存在,试求出实数
都成立?若存在,试求出实数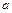 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.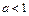
假设存在,由题意知: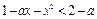 在
在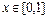 上恒成立.
上恒成立.
法1:即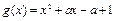 在
在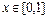 上的最小值大于0……………………………(3分)
上的最小值大于0……………………………(3分)
 .
.
若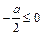 ,即
,即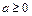 时,
时,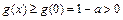 ,
,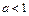 ,
,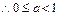 ………………………(6分)
………………………(6分)
若 即
即 时,
时,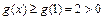 .成立………………………………………(9分)
.成立………………………………………(9分)
若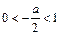 即
即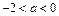 时,
时,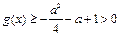 ,
,
即 ,
, .………………………………………………(12分)
.………………………………………………(12分)
综上: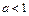 ………………………………………………………………………(13分)
………………………………………………………………………(13分)
法2:即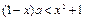 ,在
,在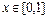 上恒成立. ………………………………(3分)
上恒成立. ………………………………(3分)
当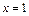 时,
时,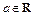 ,
,
当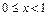 时,
时, 在
在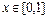 上恒成立.
上恒成立.
即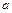 小于函数
小于函数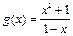 在
在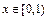 上的最小值. ………………………………(5分)
上的最小值. ………………………………(5分)

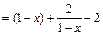 .
.
令 在
在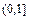 上为减函数, ………………………………(10分)
上为减函数, ………………………………(10分)
 ,
,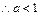 . ………………………………(13分)
. ………………………………(13分)
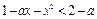 在
在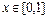 上恒成立.
上恒成立.法1:即
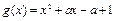 在
在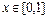 上的最小值大于0……………………………(3分)
上的最小值大于0……………………………(3分) .
.若
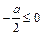 ,即
,即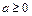 时,
时,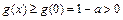 ,
,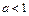 ,
,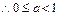 ………………………(6分)
………………………(6分)若
 即
即 时,
时,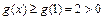 .成立………………………………………(9分)
.成立………………………………………(9分)若
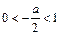 即
即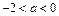 时,
时,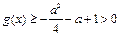 ,
,即
 ,
, .………………………………………………(12分)
.………………………………………………(12分)综上:
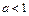 ………………………………………………………………………(13分)
………………………………………………………………………(13分)法2:即
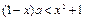 ,在
,在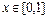 上恒成立. ………………………………(3分)
上恒成立. ………………………………(3分)当
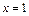 时,
时,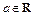 ,
, 当
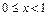 时,
时, 在
在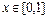 上恒成立.
上恒成立.即
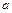 小于函数
小于函数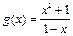 在
在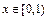 上的最小值. ………………………………(5分)
上的最小值. ………………………………(5分)
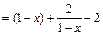 .
.令
 在
在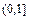 上为减函数, ………………………………(10分)
上为减函数, ………………………………(10分) ,
,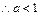 . ………………………………(13分)
. ………………………………(13分)
练习册系列答案
相关题目
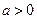 ,函数
,函数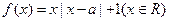 .
.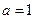 时,求所有使
时,求所有使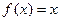 成立的
成立的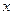 的值;
的值;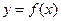 在闭区间
在闭区间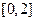 上的最大值和最小值;
上的最大值和最小值;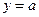 的交点个数.
的交点个数.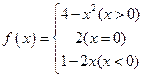 ,
, 图像;
图像;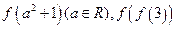 的值;
的值;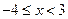 时,求
时,求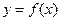 满足:①
满足:①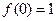 ;②
;②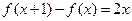 。则
。则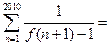 _____.
_____.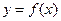 的图像如图,则满足
的图像如图,则满足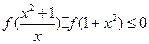 的
的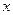 的取值范围是_______________.
的取值范围是_______________. 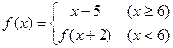 ,则f(3)为( )
,则f(3)为( )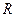 上的函数
上的函数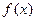 满足
满足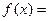
 ,
,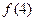 的值为 .
的值为 .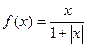 (
(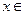 R) 时,分别给出下面几个结论:
R) 时,分别给出下面几个结论: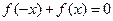 在
在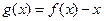 在R上有三个零点.
在R上有三个零点.