题目内容
y=f(x)在R上有定义,对于给定的正数k,定义fk(x)=
|
| 1 |
| 2 |
分析:由题意,fk(x)=
表示f(x)和k中的较小值,而
=2-1,故可分x≤-1,-1<x<1和x≥1三段进行讨论;或者作出f(x)=2-|x|的图象,与
比较大小,从而确定fk(x)的图象,由图象确定单调递增区间.
|
| 1 |
| 2 |
| 1 |
| 2 |
解答: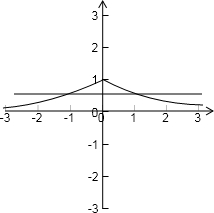 解:f(x)=2-|x|的图象和k=
解:f(x)=2-|x|的图象和k=
的图象如右图所示:
fk(x)=
表示f(x)和k中的较小值,
故fk(x)=
故fk(x)的单调递增区间为(-∞,-1]
故答案为:(-∞,-1]
 解:f(x)=2-|x|的图象和k=
解:f(x)=2-|x|的图象和k=| 1 |
| 2 |
fk(x)=
|
故fk(x)=
|
故fk(x)的单调递增区间为(-∞,-1]
故答案为:(-∞,-1]
点评:本题为新定义问题,正确理解新定义的含义是解决此类问题的关键.本题还考查含有绝对值的函数的性质问题.

练习册系列答案
相关题目
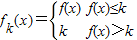 取f(x)=2-|x|,当
取f(x)=2-|x|,当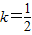 时,fk(x)的单调递增区间为 .
时,fk(x)的单调递增区间为 .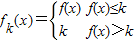 取f(x)=2-|x|,当
取f(x)=2-|x|,当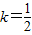 时,fk(x)的单调递增区间为 .
时,fk(x)的单调递增区间为 .