题目内容
在极坐标系中,圆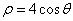 上的点到直线
上的点到直线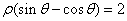 的最大距离为 .
的最大距离为 .
【答案】

【解析】
试题分析:圆 ,即ρ2=4ρcosθ,即 x2+y2=4x,
,即ρ2=4ρcosθ,即 x2+y2=4x,
(x-2)2+y2=4,表示以C(2,0)为圆心,以2为半径的圆.
直线 ,即ρsinθ-ρcosθ=2,即x-y+2=0,
,即ρsinθ-ρcosθ=2,即x-y+2=0,
,圆心C(2,0)到直线x-y+2=0的距离等于 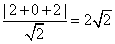 ,
,
故圆上的点到直线x-y+2=0的距离的最大值为 。
。
考点:本题主要考查简单曲线的极坐标方程与直角坐标方程的互化,直线与圆的位置关系,点到直线的距离。
点评:中档题,将曲线的极坐标方程化为直角坐标方程,实现了“化生为熟”。利用数形结合思想,将最大距离确定为圆心到直线的距离加半径。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
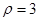 上的点到直线
上的点到直线 的距离为
的距离为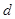 ,求
,求 上的点到直线
上的点到直线 的距离的最小值是 .
的距离的最小值是 .