题目内容
设椭圆C的中心在坐标原点O,焦点在x轴上,短轴长为2 ,左焦点到左准线的距离为3
,左焦点到左准线的距离为3 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C上有不同两点P、Q,且OP⊥OQ,过P、Q的直线为l,求点O到直线l的距离.
解:设椭圆C的方程为 +
+ =1(a>b>0),
=1(a>b>0),
则2b=2 ,b=
,b= .
.
由-c-(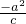 )=3
)=3 ,即
,即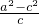 =
= =3
=3 ,得c=
,得c= .
.
于是a2=b2+c2=21+7=28,椭圆C的方程为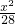 +
+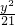 =1.(5分)
=1.(5分)
(2)若直线l的斜率不存在,即l⊥x轴时,不妨设l与x正半轴交于点M,将x=y代入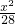 +
+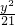 =1中,得x=y=±2
=1中,得x=y=±2 ,则点P(2
,则点P(2 ,2
,2 ),Q(2
),Q(2 ,-2
,-2 ),于是点O到l的距离为2
),于是点O到l的距离为2 .(7分)
.(7分)
若直线l的斜率存在,设l的方程为y=kx+m(k,m∈R),则点P(x1,y1),Q(x2,y2)的坐标是方程组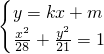 的两个实数解,
的两个实数解,
消去y,整理,得(3+4k2)x2+8kmx+4m2-84=0,
∴△=(8km)2-4(3+4k2)(4m2-84)=12(28k2-m2+21)>0,①
x1+x2=-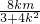 ,x1•x2=
,x1•x2=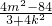 .②(9分)
.②(9分)
∵OP⊥OQ,∴kOP•kOQ=-1,即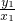 •
•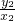 =-1,x1x2+y1y2=0.
=-1,x1x2+y1y2=0.
于是x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=0.③
将x1+x2,x1x2代入上式,得(1+k2)•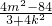 -km
-km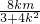 +m2=0,
+m2=0,
∴(k2+1)(4m2-84)-8k2m2+m2(4k2+3)=0,
化简,得m2=12(k2+1).④
④代入①满足,因此原点O到直线l的距离d=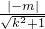 =
= =2
=2 .(12分)
.(12分)
分析:设椭圆C的方程为 +
+ =1(a>b>0),b=
=1(a>b>0),b= .由-c-(
.由-c-(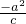 )=3
)=3 ,得c=
,得c= .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.
(2)若直线l的斜率不存在,设l与x正半轴交于点M,将x=y代入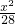 +
+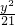 =1中,得到点P(2
=1中,得到点P(2 ,2
,2 ),Q(2
),Q(2 ,-2
,-2 ),于是点O到l的距离为2
),于是点O到l的距离为2 .若直线l的斜率存在,设l的方程为y=kx+m(k,m∈R),则点P(x1,y1),Q(x2,y2)的坐标是方程组
.若直线l的斜率存在,设l的方程为y=kx+m(k,m∈R),则点P(x1,y1),Q(x2,y2)的坐标是方程组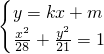 的两个实数解,再由根的判别式和韦达定理进行求解.
的两个实数解,再由根的判别式和韦达定理进行求解.
点评:本题考查椭圆的性质和应用,解题时要认真审题,仔细解答,注意合理地选用公式.
 +
+ =1(a>b>0),
=1(a>b>0),则2b=2
 ,b=
,b= .
.由-c-(
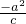 )=3
)=3 ,即
,即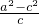 =
= =3
=3 ,得c=
,得c= .
.于是a2=b2+c2=21+7=28,椭圆C的方程为
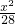 +
+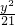 =1.(5分)
=1.(5分)(2)若直线l的斜率不存在,即l⊥x轴时,不妨设l与x正半轴交于点M,将x=y代入
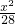 +
+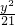 =1中,得x=y=±2
=1中,得x=y=±2 ,则点P(2
,则点P(2 ,2
,2 ),Q(2
),Q(2 ,-2
,-2 ),于是点O到l的距离为2
),于是点O到l的距离为2 .(7分)
.(7分)若直线l的斜率存在,设l的方程为y=kx+m(k,m∈R),则点P(x1,y1),Q(x2,y2)的坐标是方程组
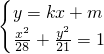 的两个实数解,
的两个实数解,消去y,整理,得(3+4k2)x2+8kmx+4m2-84=0,
∴△=(8km)2-4(3+4k2)(4m2-84)=12(28k2-m2+21)>0,①
x1+x2=-
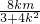 ,x1•x2=
,x1•x2=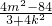 .②(9分)
.②(9分)∵OP⊥OQ,∴kOP•kOQ=-1,即
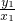 •
•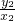 =-1,x1x2+y1y2=0.
=-1,x1x2+y1y2=0.于是x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=0.③
将x1+x2,x1x2代入上式,得(1+k2)•
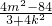 -km
-km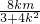 +m2=0,
+m2=0,∴(k2+1)(4m2-84)-8k2m2+m2(4k2+3)=0,
化简,得m2=12(k2+1).④
④代入①满足,因此原点O到直线l的距离d=
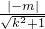 =
= =2
=2 .(12分)
.(12分)分析:设椭圆C的方程为
 +
+ =1(a>b>0),b=
=1(a>b>0),b= .由-c-(
.由-c-(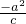 )=3
)=3 ,得c=
,得c= .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.(2)若直线l的斜率不存在,设l与x正半轴交于点M,将x=y代入
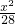 +
+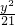 =1中,得到点P(2
=1中,得到点P(2 ,2
,2 ),Q(2
),Q(2 ,-2
,-2 ),于是点O到l的距离为2
),于是点O到l的距离为2 .若直线l的斜率存在,设l的方程为y=kx+m(k,m∈R),则点P(x1,y1),Q(x2,y2)的坐标是方程组
.若直线l的斜率存在,设l的方程为y=kx+m(k,m∈R),则点P(x1,y1),Q(x2,y2)的坐标是方程组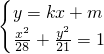 的两个实数解,再由根的判别式和韦达定理进行求解.
的两个实数解,再由根的判别式和韦达定理进行求解.点评:本题考查椭圆的性质和应用,解题时要认真审题,仔细解答,注意合理地选用公式.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
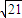 ,左焦点到左准线的距离为3
,左焦点到左准线的距离为3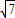 .
.