Question

若x，y满足|ax|+|y|≤1（a＞0），设x2+y2+

2

a

x+2y的最小值为f（a），最大值为g（a），如果9[f(a)+1+

1

a2

]＞g(a)，则a的取值范围是

 

．

Answer 1

分析：由x，y满足|ax|+|y|≤1（a＞0），画出图象：令t=x2+y2+

2

a

x+2y=(x+

1

a

)2+(y+1)2-1-

1

a2

，
设圆：(x+

1

a

)2+(y-1)2=r2．分类讨论：①当0＜a＜1时，当取点(

1

a

，0)时，t取得最大值，可得g（a）=

3

a2

．
当圆与直线-ax-y=1相切时，t取得最小值，利用点到直线的距离公式可得r=

|-1+1+1|

a2+1

，于是f（a）=

1

a2+1

-1-

1

a2

．再利用9[f(a)+1+

1

a2

]＞g(a)，即可解得．②当a=1时，经验证满足条件，因此a=1．③当a＞1时，类比①可得：f（a）=

1

a2+1

-1-

1

a2

；当取点（0，1）时，t取得最大值，g（a）=3．
再利用9[f(a)+1+

1

a2

]＞g(a)，即可解得．

解答：解：由x，y满足|ax|+|y|≤1（a＞0），画出图象：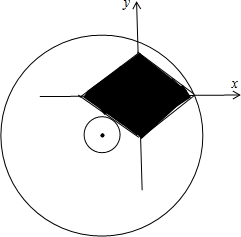
令t=x2+y2+

2

a

x+2y=(x+

1

a

)2+(y+1)2-1-

1

a2

，
设圆：(x+

1

a

)2+(y-1)2=r2．
①当0＜a＜1时，当取点(

1

a

，0)时，t取得最大值，
∴g（a）=(

2

a

)2+1-1-

1

a2

=

3

a2

．
当圆与直线-ax-y=1相切时，t取得最小值，
r=

|-1+1+1|

a2+1

，
∴f（a）=

1

a2+1

-1-

1

a2

．
∵9[f(a)+1+

1

a2

]＞g(a)，∴

9

a2+1

＞

3

a2

，化为2a²＞1．
又0＜a＜1，解得

2

2

＜a＜1．
②当a=1时，经验证满足条件，因此a=1．
③当a＞1时，类比①可得：f（a）=

1

a2+1

-1-

1

a2

；
当取点（0，1）时，t取得最大值，
∴g（a）=3．
∵9[f(a)+1+

1

a2

]＞g(a)，∴

9

1+a2

＞3，化为a²＜2．
又a＞1，解得1＜a＜

2

．
综上可知：a的取值范围是(

2

2

，

2

)．
故答案为：(

2

2

，

2

)．

点评：本题综合考查了线性规划问题、直线与圆相切问题、分类讨论等基础知识与基本技能方法，考查了分析问题和解决问题的能力，考查了计算能力，属于难题．