题目内容
对于两个定义域相同的函数f(x),g(x),若存在实数m、n使h(x)=mf(x)+ng(x),则称函数h(x)是由“基函数f(x),g(x)”生成的.(1)若f(x)=x2+3x和个g(x)=3x+4生成一个偶函数h(x),求h(2)的值;
(2)若h(x)=2x2+3x-1由函数f(x)=x2+ax,g(x)=x+b(a、b∈R且ab≠0)生成,求a+2b的取值范围;
(3)试利用“基函数f(x)=log4(4+1)、g(x)=x-1”生成一个函数h(x),使之满足下列件:①是偶函数;②有最小值1;求函数h(x)的解析式并进一步研究该函数的单调性(无需证明).
【答案】分析:(1)先用待定系数法表示出偶函数h(x),再根据其是偶函数这一性质得到引入参数的方程,求出参数的值,即得函数的解析式,代入自变量求值即可.
(2)先用待定系数法表示出偶函数h(x),再根据同一性建立引入参数的方程求参数,然后再求a+2b的取值范围;
(3)先用待定系数法表示出函数h(x),再根据函数h(x)的性质求出相关的参数,代入解析式,由解析研究出其单调性即可
解答:解:(1)设h(x)=m(x2+3x)+n(3x+4)=mx2+3(m+n)x+4n,
∵h(x)是偶函数,∴m+n=0,∴h(2)=4m+4n=0;(4分)
(2)设h(x)=2x2+3x-1=m(x2+ax)+n(x+b)=mx2+(am+n)x+nb
∴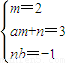 得
得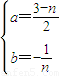
∴a+2b=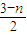 -
-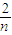 =
= -
-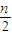 -
-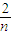 (8分)
(8分)
由ab≠0知,n≠3,
∴a+2b∈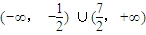 (11分)
(11分)
(3)设h(x)=mlog4(4x+1)+n(x-1)
∵h(x)是偶函数,∴h(-x)-h(x)=0,
即mlog4(4-x+1)+n(-x-1)-mlog4(4x+1)-n(x-1)=0
∴(m+2n)x=0得m=-2n(13分)
则h(x)=-2nlog4(4x+1)+n(x-1)=-2n[log4(4x+1)-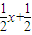 ]=-2n[log4(2x+
]=-2n[log4(2x+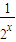 )+
)+ ]
]
∵h(x)有最小值1,则必有n<0,且有-2n=1∴m=1.n=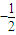
∴h(x)=log4(2x+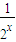 )+
)+
h(x)在[0,+∞)上是增函数,在(-∞,0]上是减函数.(18分)
点评:本题考点是函数的奇偶性与单调性综合,考查了利用偶函数建立方程求参数以及利用同一性建立方程求参数,本题涉及到函数的性质较多,综合性,抽象性很强,做题时要做到每一步变化严谨,才能保证正确解答本题.
(2)先用待定系数法表示出偶函数h(x),再根据同一性建立引入参数的方程求参数,然后再求a+2b的取值范围;
(3)先用待定系数法表示出函数h(x),再根据函数h(x)的性质求出相关的参数,代入解析式,由解析研究出其单调性即可
解答:解:(1)设h(x)=m(x2+3x)+n(3x+4)=mx2+3(m+n)x+4n,
∵h(x)是偶函数,∴m+n=0,∴h(2)=4m+4n=0;(4分)
(2)设h(x)=2x2+3x-1=m(x2+ax)+n(x+b)=mx2+(am+n)x+nb
∴
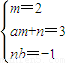 得
得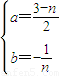
∴a+2b=
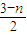 -
-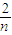 =
= -
-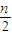 -
-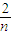 (8分)
(8分)由ab≠0知,n≠3,
∴a+2b∈
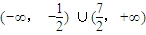 (11分)
(11分)(3)设h(x)=mlog4(4x+1)+n(x-1)
∵h(x)是偶函数,∴h(-x)-h(x)=0,
即mlog4(4-x+1)+n(-x-1)-mlog4(4x+1)-n(x-1)=0
∴(m+2n)x=0得m=-2n(13分)
则h(x)=-2nlog4(4x+1)+n(x-1)=-2n[log4(4x+1)-
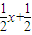 ]=-2n[log4(2x+
]=-2n[log4(2x+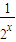 )+
)+ ]
]∵h(x)有最小值1,则必有n<0,且有-2n=1∴m=1.n=
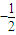
∴h(x)=log4(2x+
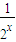 )+
)+
h(x)在[0,+∞)上是增函数,在(-∞,0]上是减函数.(18分)
点评:本题考点是函数的奇偶性与单调性综合,考查了利用偶函数建立方程求参数以及利用同一性建立方程求参数,本题涉及到函数的性质较多,综合性,抽象性很强,做题时要做到每一步变化严谨,才能保证正确解答本题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目