题目内容
已知实数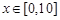 ,若执行如下左图所示的程序框图,则输出的
,若执行如下左图所示的程序框图,则输出的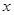 不小于 47的概率为( )
不小于 47的概率为( )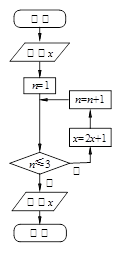
A.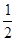 | B.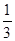 | C.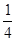 | D.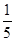 |
A
解析试题分析:设实数x∈[0,10],
经过第一次循环得到x=2x+1,n=2,
经过第二循环得到x=2(2x+1)+1,n=3,
经过第三次循环得到x=2[2(2x+1)+1]+1,n=3此时输出x,
输出的值为8x+7,令8x+7≥47得x≥5。
由几何概型得到输出的x不小于47的概率为P=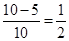 ,故选A。
,故选A。
考点:本题主要考查程序框图的功能识别,简单不等式解法,几何概型概率的计算。
点评:基础题,程序框图的功能识别,是近些年常考的题目,一般不难。往往和函数、数列、方程、概率、不等式等结合,以扩大知识覆盖面。

练习册系列答案
相关题目
阅读右边的程序框图,运行相应的程序,输出的结果为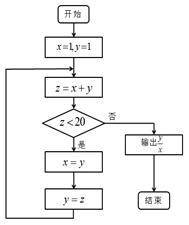
A.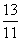 | B.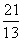 | C.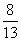 | D.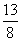 |
下图所示的程序的输出结果为sum=132,则判断框中应填( )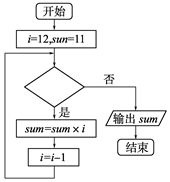
| A.i≥10 | B.i≥11 | C.i≤11 | D.i≥12 |
某程序框图如图所示,该程序框图的功能是 ( )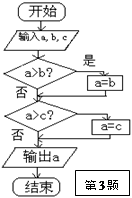
| A.求输出a,b,c三数的最大数 |
| B.求输出a,b,c三数的最小数 |
| C.将a,b,c按从小到大排列 |
| D.将a,b,c按从大到小排列 |
下面程序运行后,a,b,c的值各等于 ( )
a = 3
b =" -" 5
c = 8
a = b
b = c
c = a
PRINT a, b, c
END
| A.–5,8,-5 | B.–5,8,3 | C.8,–5,3 | D.8,–5,8 |
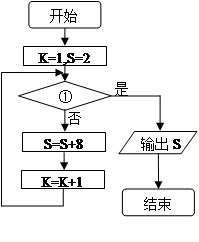
若右边的程序框图输出的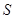 是
是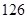 ,则条件①可为
,则条件①可为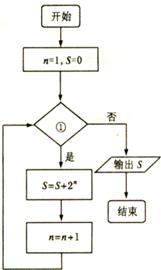
A.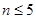 | B.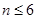 | C.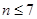 | D.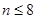 |
执行右面的程序框图,若输入的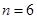 ,
,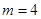 ,那么输出的
,那么输出的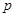 是
是
| A.120 | B.240 | C.360 | D.720 |
右边程序的输出结果为
| A.15,1 | B.15,7 |
| C.56,8 | D.120,8 |