题目内容
已知函数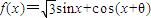 的定义域为R,最大值为1(其中θ为常数,且
的定义域为R,最大值为1(其中θ为常数,且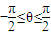 ).
).(1)求角θ的值;
(2)若f(x)=1,求cos2x的值.
【答案】分析:(1)先利用余弦的和角公式展开,然后利用辅助角公式可求得函数的最大值,建立关于sinθ和cosθ的方程,再根据同角三角函数关系,可求出角θ的值;
(2)由(1)可求出函数f(x)的解析式,然后根据f(x)=1建立等式关系,最后解三角方程求出x的值,代入cos2x求出其值即可.
解答:解:(1)由 (θ为常数)
(θ为常数)
=
=

依题意知:
化简为:
又 ,故
,故 …(6分)
…(6分)
(2)由(1)可知
∴ ∴
∴ .
.
∴
∴ .…(12分)
.…(12分)
点评:本题主要考查了三角函数的最值,以及辅助角公式的应用和三角方程的求解,属于基础题.
(2)由(1)可求出函数f(x)的解析式,然后根据f(x)=1建立等式关系,最后解三角方程求出x的值,代入cos2x求出其值即可.
解答:解:(1)由
 (θ为常数)
(θ为常数)=

=


依题意知:

化简为:

又
 ,故
,故 …(6分)
…(6分)(2)由(1)可知

∴
 ∴
∴ .
.∴

∴
 .…(12分)
.…(12分)点评:本题主要考查了三角函数的最值,以及辅助角公式的应用和三角方程的求解,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
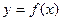 的定义域为R,且当
的定义域为R,且当 时,
时,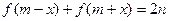 恒成立,
恒成立,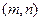 对称;
对称; 图象的一个对称点。
图象的一个对称点。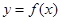 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数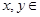 R,等式
R,等式 成立.若数列
成立.若数列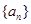 满足
满足 ,且
,且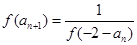
 N*),则
N*),则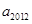 的值为( )
的值为( ) 的定义域为R,它的反函数为
的定义域为R,它的反函数为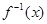 ,如果
,如果 与
与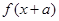 互为反函数,且
互为反函数,且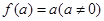 ,则
,则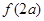 的值为(
)
的值为(
)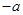 B、0
C、
B、0
C、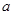 D、
D、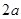
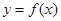 的定义域为R,当
的定义域为R,当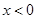 时,
时, ,且对任意的实数
,且对任意的实数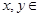 R,等式
R,等式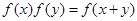 成立.若数列
成立.若数列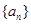 满足
满足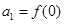 ,且
,且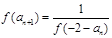 (
(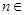 N*),则
N*),则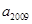 的值为( )
的值为( )