题目内容
将所有平面向量组成的集合记作R2,f是从R2到R2的映射,记作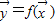 或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|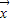 |=1的条件下|
|=1的条件下|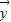 |的最大值,记做||f||.若存在非零向量
|的最大值,记做||f||.若存在非零向量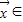 R2,及实数λ使得f(
R2,及实数λ使得f(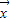 )=
)=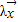 ,则称λ为f的一个特征值.
,则称λ为f的一个特征值.(1)若f(x1,x2)=(
 x1,x2),求||f||;
x1,x2),求||f||;(2)如果f(x1,x2)=(x1+x2,x1-x2),计算f的特征值,并求相应的
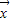 ;
;(3)若f(x1,x2)=(a1x1+a2x2,b1x1+b2x2),要使f有唯一的特征值,实数a1,a2,b1,b2应满足什么条件?试找出一个映射f,满足以下两个条件:①有唯一的特征值λ,②||f||=|λ|,并验证f满足这两个条件.
【答案】分析:(1)由新定义可得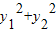 =
=
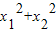 ,利用
,利用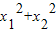 =1,可得
=1,可得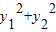 ≤1,从而可得结论;
≤1,从而可得结论;
(2)由特征值的定义可得: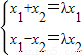 ,由此可得f的特征值,及相应的
,由此可得f的特征值,及相应的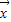 ;
;
(3)解方程组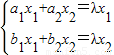 ,可得x1(a1-λ,b1)+x2(a2,-b1-λ)=0,从而可得a1,a2,b1,b2应满足的条件,当f(
,可得x1(a1-λ,b1)+x2(a2,-b1-λ)=0,从而可得a1,a2,b1,b2应满足的条件,当f(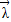 )=λ
)=λ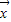 时,f有唯一的特征值,且||f||=|λ|,再进行证明即可.
时,f有唯一的特征值,且||f||=|λ|,再进行证明即可.
解答:解:(1)由于此时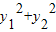 =
=
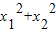 ,
,
又因为是在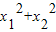 =1的条件下,有
=1的条件下,有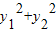 =
=
 =
=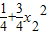 ≤1(x2=±1时取最大值),
≤1(x2=±1时取最大值),
所以此时有||f||=1;…(4分)
(2)由f(x1,x2)=(x1+x2,x1-x2)=λ(x1,x2),可得: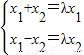 ,
,
解此方程组可得:(λ-1)(λ+1)=1,从而λ=±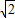 .
.
当λ=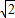 时,解方程组
时,解方程组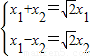 ,此时这两个方程是同一个方程,
,此时这两个方程是同一个方程,
所以此时方程有无穷多个解,为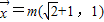 (写出一个即可),其中m∈R且m≠0.
(写出一个即可),其中m∈R且m≠0.
当λ=-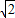 时,同理可得,相应的
时,同理可得,相应的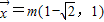 (写出一个即可),其中m∈R且m≠0.…(9分)
(写出一个即可),其中m∈R且m≠0.…(9分)
(3)解方程组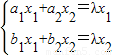 ,可得x1(a1-λ,b1)+x2(a2,-b1-λ)=0
,可得x1(a1-λ,b1)+x2(a2,-b1-λ)=0
从而向量(a1-λ,b1)与(a2,-b1-λ)平行,
从而有a1,a2,b1,b2应满足: .
.
当f(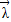 )=λ
)=λ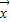 时,f有唯一的特征值,且||f||=|λ|.具体证明为:
时,f有唯一的特征值,且||f||=|λ|.具体证明为:
由f的定义可知:f(x1,x2)=λ(x1,x2),所以λ为特征值.
此时a1=λ,a2=0,b1=0,b2=λ满足: ,所以有唯一的特征值.
,所以有唯一的特征值.
在 =1的条件下
=1的条件下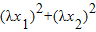 =λ2,从而有||f||=|λ|.…(14分)
=λ2,从而有||f||=|λ|.…(14分)
点评:本题考查新定义,考查学生的计算能力,考查学生分析解决问题的能力,正确运用新定义是关键.
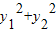 =
=
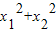 ,利用
,利用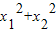 =1,可得
=1,可得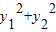 ≤1,从而可得结论;
≤1,从而可得结论;(2)由特征值的定义可得:
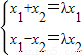 ,由此可得f的特征值,及相应的
,由此可得f的特征值,及相应的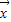 ;
;(3)解方程组
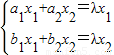 ,可得x1(a1-λ,b1)+x2(a2,-b1-λ)=0,从而可得a1,a2,b1,b2应满足的条件,当f(
,可得x1(a1-λ,b1)+x2(a2,-b1-λ)=0,从而可得a1,a2,b1,b2应满足的条件,当f(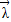 )=λ
)=λ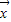 时,f有唯一的特征值,且||f||=|λ|,再进行证明即可.
时,f有唯一的特征值,且||f||=|λ|,再进行证明即可.解答:解:(1)由于此时
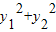 =
=
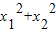 ,
,又因为是在
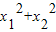 =1的条件下,有
=1的条件下,有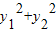 =
=
 =
=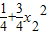 ≤1(x2=±1时取最大值),
≤1(x2=±1时取最大值),所以此时有||f||=1;…(4分)
(2)由f(x1,x2)=(x1+x2,x1-x2)=λ(x1,x2),可得:
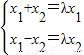 ,
,解此方程组可得:(λ-1)(λ+1)=1,从而λ=±
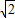 .
.当λ=
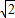 时,解方程组
时,解方程组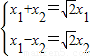 ,此时这两个方程是同一个方程,
,此时这两个方程是同一个方程,所以此时方程有无穷多个解,为
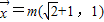 (写出一个即可),其中m∈R且m≠0.
(写出一个即可),其中m∈R且m≠0.当λ=-
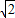 时,同理可得,相应的
时,同理可得,相应的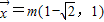 (写出一个即可),其中m∈R且m≠0.…(9分)
(写出一个即可),其中m∈R且m≠0.…(9分)(3)解方程组
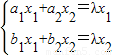 ,可得x1(a1-λ,b1)+x2(a2,-b1-λ)=0
,可得x1(a1-λ,b1)+x2(a2,-b1-λ)=0从而向量(a1-λ,b1)与(a2,-b1-λ)平行,
从而有a1,a2,b1,b2应满足:
 .
.当f(
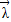 )=λ
)=λ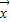 时,f有唯一的特征值,且||f||=|λ|.具体证明为:
时,f有唯一的特征值,且||f||=|λ|.具体证明为:由f的定义可知:f(x1,x2)=λ(x1,x2),所以λ为特征值.
此时a1=λ,a2=0,b1=0,b2=λ满足:
 ,所以有唯一的特征值.
,所以有唯一的特征值.在
 =1的条件下
=1的条件下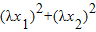 =λ2,从而有||f||=|λ|.…(14分)
=λ2,从而有||f||=|λ|.…(14分)点评:本题考查新定义,考查学生的计算能力,考查学生分析解决问题的能力,正确运用新定义是关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
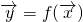 或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在| |=1的条件下|
|=1的条件下| |的最大值,记做||f||.若存在非零向量
|的最大值,记做||f||.若存在非零向量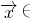 R2,及实数λ使得f(
R2,及实数λ使得f(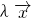 ,则称λ为f的一个特征值.
,则称λ为f的一个特征值. x1,x2),求||f||;
x1,x2),求||f||;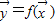 或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|
或(y1,y2)=f(x1,x2),其中x1,x2,y1,y2都是实数.定义映射f的模为:在|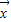 |=1的条件下|
|=1的条件下|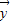 |的最大值,记做||f||.若存在非零向量
|的最大值,记做||f||.若存在非零向量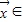 R2,及实数λ使得f(
R2,及实数λ使得f(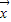 )=
)=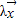 ,则称λ为f的一个特征值.
,则称λ为f的一个特征值. x1,x2),求||f||;
x1,x2),求||f||;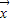 ;
;