题目内容
设定义在R的函数f(x)同时满足以下条件:①f(x)+f(-x)=0;②f(x)=f(x+2);③当0≤x<1时,f(x)=2x-1.则f(| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
分析:根据f(x)是定义在R上的函数且f(x)+f(-x)=0,求得f(0)=0,进而根据f(x)=f(x+2)求得f(1)和f(2)的值,进而利用当0≤x<1时,f(x)的解析式求得f(
)的值,利用函数的周期性求得f(
)=f(
),f(
)=-f(
),进而分别求得f(
)和f(
)的值.代入f(
)+f(1)+f(
)+f(2)+f(
)中求得答案.
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
解答:解:由f(x)是定义在R上的函数且f(x)+f(-x)=0,
所以f(0)=0,又f(x)=f(x+2)
所以f(1)=f(-1)=-f(1)?f(1)=0且f(2)=f(0)=0,
f(
)=2
-1=
-1,
f(
)=f(
),
f(
)=f(-
)=-f(
)
∴f(
)+f(1)+f(
)+f(2)+f(
)=f(
)=
-1.
故答案为:
-1
所以f(0)=0,又f(x)=f(x+2)
所以f(1)=f(-1)=-f(1)?f(1)=0且f(2)=f(0)=0,
f(
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
f(
| 5 |
| 2 |
| 1 |
| 2 |
f(
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题主要考查了函数的周期性和奇偶性的应用.解题的过程要特别留意函数解析式的定义域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
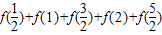 = .
= .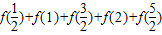 = .
= .