题目内容
对于如下四个函数:①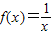 ,②f(x)=|x|,③f(x)=2,④f(x)=x2.
,②f(x)=|x|,③f(x)=2,④f(x)=x2.其中满足性质:“对于区间(1,2)上的任意x1,x2(x1≠x2),|f(x2)-f(x1)|<|x2-x1|恒成立”的函数为 .
【答案】分析:把4个选项中的函数分别代入不等式|f(x2)-f(x1)|<|x2-x1|分别验证是否成立即可得到答案.
解答:解:在区间(1,2)上的任意实数x1,x2(x1≠x2),分别验证下列4个函数.
对于①: f(x)=,|f(x2)-f(x1)|=|
f(x)=,|f(x2)-f(x1)|=|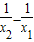 |=|
|=|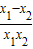 |<|x2-x1|(因为x1,x2在区间(1,2)上,故x1x2大于1)故成立.
|<|x2-x1|(因为x1,x2在区间(1,2)上,故x1x2大于1)故成立.
对于②:f(x)=|x|,|f(x2)-f(x1)|=||x2|-|x1||=|x2-x1|,故不成立.
对于③:f(x)=2,|f(x2)-f(x1)|=0,∵x1≠x2,∴0<|x2-x1|,故成立.
对于④:f(x)=x2,|f(x2)-f(x1)|=|x22-x12|=(x2+x1)|x2-x1|>|x2-x1|,故不成立.
故答案为:①③.
点评:本题考查新定义,考查绝对值不等式的应用问题.对于此类型的题目需要对题目选项一个一个做分析,然后用排除法作答即可,属于中档题.
解答:解:在区间(1,2)上的任意实数x1,x2(x1≠x2),分别验证下列4个函数.
对于①:
 f(x)=,|f(x2)-f(x1)|=|
f(x)=,|f(x2)-f(x1)|=|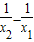 |=|
|=|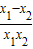 |<|x2-x1|(因为x1,x2在区间(1,2)上,故x1x2大于1)故成立.
|<|x2-x1|(因为x1,x2在区间(1,2)上,故x1x2大于1)故成立.对于②:f(x)=|x|,|f(x2)-f(x1)|=||x2|-|x1||=|x2-x1|,故不成立.
对于③:f(x)=2,|f(x2)-f(x1)|=0,∵x1≠x2,∴0<|x2-x1|,故成立.
对于④:f(x)=x2,|f(x2)-f(x1)|=|x22-x12|=(x2+x1)|x2-x1|>|x2-x1|,故不成立.
故答案为:①③.
点评:本题考查新定义,考查绝对值不等式的应用问题.对于此类型的题目需要对题目选项一个一个做分析,然后用排除法作答即可,属于中档题.

练习册系列答案
相关题目
 ,②f(x)=|x|,③f(x)=2,④f(x)=x2.
,②f(x)=|x|,③f(x)=2,④f(x)=x2.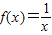 ,②f(x)=|x|,③f(x)=2,④f(x)=x2.
,②f(x)=|x|,③f(x)=2,④f(x)=x2.