题目内容
已知双曲线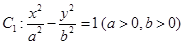 的左、右焦点分别为
的左、右焦点分别为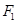 、
、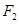 ,抛物线
,抛物线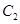 的顶点在原点,它的准线与双曲线
的顶点在原点,它的准线与双曲线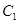 的左准线重合,若双曲线
的左准线重合,若双曲线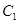 与抛物线
与抛物线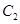 的交点
的交点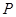 满足
满足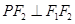 ,则双曲线
,则双曲线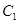 的离心率为
的离心率为
| A. | B. | C. | D.2 |
B
解析考点:双曲线的简单性质.
分析:先设出抛物线方程,进而根据题意可得p与a和c的关系,把抛物线方程与双曲线方程联立,把x=c,p="2" 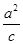 ,代入整理可得答案.
,代入整理可得答案.
解:设抛物线方程为y2=2px,依题意可知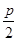 =
=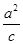
∴p=2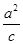 ,
,
抛物线方程与双曲线方程联立得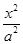 -
-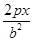 =1,把x=c,p=2
=1,把x=c,p=2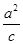 ,代入整理得e4-2e2-3=0
,代入整理得e4-2e2-3=0
解得e2=3或-1(舍去)
∴e=
故选B。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
若椭圆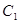 :
: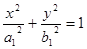 (
( )和椭圆
)和椭圆 :
: 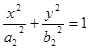
(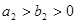 )的焦点相同且
)的焦点相同且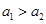 .给出如下四个结论:
.给出如下四个结论:
①椭圆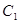 和椭圆
和椭圆 一定没有公共点; ②
一定没有公共点; ② ;
;
③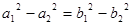 ; ④
; ④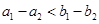 .
.
其中,所有正确结论的序号是( )
| A.②③④ | B.①③④ | C.①②④ | D.①②③ |
已知双曲线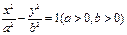 的两个焦点分别为
的两个焦点分别为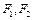 ,过作垂直于x轴的直线,
,过作垂直于x轴的直线,
与双曲线的一个交点为P,且 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
| A.2 | B. | C.3 | D.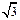 |
若焦点在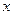 轴上的椭圆
轴上的椭圆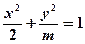 的离心率为
的离心率为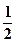 ,则m=( )
,则m=( )
A.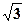 | B.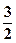 | C.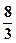 | D.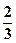 |
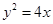 的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使
的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使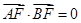 ,则直线AB的斜率
,则直线AB的斜率 ( )
( )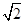 B
B 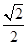 C
C  D
D 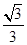
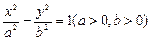 的左焦点
的左焦点 作圆
作圆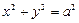 的切线,
的切线,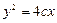 于点P,若E为线段FP的中点,则双曲线的离心率
于点P,若E为线段FP的中点,则双曲线的离心率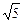
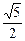

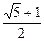

 的右焦点F作圆
的右焦点F作圆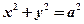 的切线FM(切点为M),交y轴于点P,若M为线段FP的中点, 则双曲线的离心率是( )
的切线FM(切点为M),交y轴于点P,若M为线段FP的中点, 则双曲线的离心率是( )
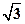
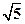
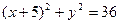 ,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q,则点Q(x,y)所满足的轨迹方程为( ▲ )
,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于点Q,则点Q(x,y)所满足的轨迹方程为( ▲ )