题目内容
设a,b∈R,|a-b|>2,则关于实数x的不等式|x-a|+|x-b|>2的解集是 .
R
解析【解题指南】利用绝对值不等式的基本知识|x-a|+|x-b|表示数轴上某点到a,b的距离之和即可得解.
解:函数f(x)=|x-a|+|x-b|的值域为:
[|a-b|,+∞).因此,当?x∈R时,f(x)≥|a-b|>2.
所以,不等式|x-a|+|x-b|>2的解集为R.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
已知x+2y+3z=6,则2x+4y+8z的最小值为 ( )
A.3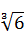 | B.2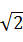 | C.12 | D.12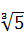 |
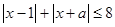 的解集不是空集,则a的最小值是__________。
的解集不是空集,则a的最小值是__________。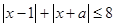 的解集不是空集,则a的最小值是__________。
的解集不是空集,则a的最小值是__________。 =x-y,则x的取值范围是 .
=x-y,则x的取值范围是 . ,若|m-1|·m=|m-1|,则m的取值范围是 .
,若|m-1|·m=|m-1|,则m的取值范围是 . 均不小于1,且
均不小于1,且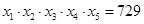 ,则
,则 的最小值是 .(
的最小值是 .(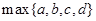 是指
是指 四个数中最大的一个)
四个数中最大的一个)