题目内容
一物体作直线运动，其运动方程为s=3t-t2，其中位移s单位为米，时间t的单位为秒，那么该物体的初速度为（ ）
分析：根据导数的物理意义可知，物体运动的瞬时速度是位移s与时间t的函数的导数，所以对位移公式求导，而初速度就是时间取第一个值0时的瞬时速度，所以只需求出t等于0时的瞬时速度即可．
解答：解：∵位移s与时间t的关系为s=3t-t2，
∴s′=3-2t，
当t=0时，s′=3，
∴物体的初速度为3
故选C．
∴s′=3-2t，
当t=0时，s′=3，
∴物体的初速度为3
故选C．
点评：本题的考点是变化的快慢与变化率，主要考查导数的物理意义，理解物体运动的瞬时速度是位移s与时间t的函数的导数时解题的关键．
练习册系列答案
相关题目
，其初速度为（ ）
B．
C．
D．
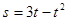，其中位移s单位为米，时间t的单