题目内容
已知向量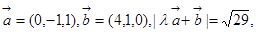 且
且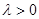 ,则
,则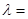
3
解析试题分析:因为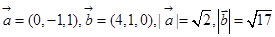 ,
, ,又因为
,又因为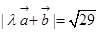 ,所以
,所以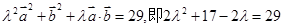 ,解得
,解得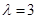 。
。
考点:空间向量的简单性质;空间向量的数量积。
点评:我们要熟记:向量的平方就等于其模的平方。一般有向量的模的时候要用到这一条。

练习册系列答案
相关题目
题目内容
已知向量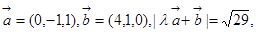 且
且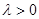 ,则
,则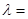
3
解析试题分析:因为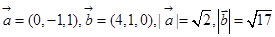 ,
, ,又因为
,又因为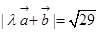 ,所以
,所以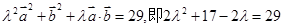 ,解得
,解得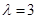 。
。
考点:空间向量的简单性质;空间向量的数量积。
点评:我们要熟记:向量的平方就等于其模的平方。一般有向量的模的时候要用到这一条。
