题目内容
(08年长沙市模拟理)(13分)已知数列{an}的前n项和Sn满足Sn=-1,Sn+1+2Sn=-1(![]() ),数列{bn}的通项公式为
),数列{bn}的通项公式为![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
解析:解析:(1)![]() ,
,
两式相减得![]()
又![]()
![]() ,即数列
,即数列![]() 是首项为-1,公比为-2的等比数列其通项公式是
是首项为-1,公比为-2的等比数列其通项公式是![]() 4分
4分
(2)不存在圆心在x轴上的圆C及互不相等的正整数n、m、k,使得三点An,Am,Ak落在圆C上。 5分
假设存在圆心在x轴上的圆C及互不相等的正整数n、m、k,使得点三点An,Am,Ak,即![]() 落在圆C上,不妨设n>m>k,设圆方程为:
落在圆C上,不妨设n>m>k,设圆方程为:
x2+y2+Dx+F=0,从而9n2-24n+16+4n-1+(3n-4)D+F=0①
9m2-24m+16+4m-1+(3m+4)D+F=0,②
9k2-24k+16+4k-1+(3k-4)D+F=0,③ 7分
由①-②,②-③得:9(n+m)(n-m)-24(n-m)+(4n-1-4m-1)+3(n-m)D=0,
9(m+k)(m-k)-24(m-k)+(4m-1-4k-1)+3(m-k)D=0,
即![]() ④
④
![]() ,⑤
,⑤
由④-⑤,得![]() ,
,
整理,得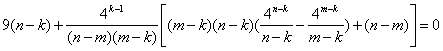 ,
,
![]() ,
,
⑥ 9分
设函数![]() ,
,
知函数![]() 是增函数
是增函数
![]() ,与⑥式产生矛盾。
,与⑥式产生矛盾。
故不存在圆心在x轴上的圆C及互不相等的正整数n、m、k,使得三点An,Am,Ak落在圆C上。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目