题目内容
已知条件p: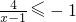 ,条件q:x2+x<a2-a,且p为q的一个必要不充分条件,则a的取值范围是
,条件q:x2+x<a2-a,且p为q的一个必要不充分条件,则a的取值范围是
- A.
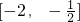
- B.[-1,2]
- C.

- D.
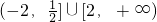
B
分析:化简条件p和条件q,由p为q的一个必要不充分条件可得,条件q中x的范围是条件p中x的范围的子集,由此求得到a的取值范围.
解答:条件p: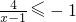 ,即
,即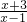 ≤0,
≤0, ,解得-3≤x<1.
,解得-3≤x<1.
条件q:x2+x<a2-a,即(x+a)[(x+(1-a)]<0.
当-a>-(1-a)时,即a< 时,条件q:a-1<x<-a,根据p为q的一个必要不充分条件,
时,条件q:a-1<x<-a,根据p为q的一个必要不充分条件,
可得(a-1,-a )?[-3,1),故有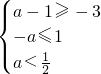 ,解得-1≤a<
,解得-1≤a< .
.
当-a<-(1-a)时,即a> ,条件q:-a<x<-(1-a) 由题意可得(-a,a-1)?[-3,1),
,条件q:-a<x<-(1-a) 由题意可得(-a,a-1)?[-3,1),
故有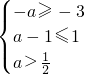 ,解得
,解得  <a≤2.
<a≤2.
当-a=-(1-a)时,即a= ,条件q:x∈∅,显然满足p为q的一个必要不充分条件.
,条件q:x∈∅,显然满足p为q的一个必要不充分条件.
综上可得,-1≤a≤2,即a的取值范围是[-1,2].
故选B.
点评:本题主要考查充分条件、必要条件、充要条件的定义和判断方法,分式不等式和一元二次不等式的解法,属于中档题
分析:化简条件p和条件q,由p为q的一个必要不充分条件可得,条件q中x的范围是条件p中x的范围的子集,由此求得到a的取值范围.
解答:条件p:
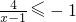 ,即
,即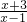 ≤0,
≤0, ,解得-3≤x<1.
,解得-3≤x<1.条件q:x2+x<a2-a,即(x+a)[(x+(1-a)]<0.
当-a>-(1-a)时,即a<
 时,条件q:a-1<x<-a,根据p为q的一个必要不充分条件,
时,条件q:a-1<x<-a,根据p为q的一个必要不充分条件,可得(a-1,-a )?[-3,1),故有
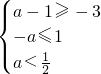 ,解得-1≤a<
,解得-1≤a< .
.当-a<-(1-a)时,即a>
 ,条件q:-a<x<-(1-a) 由题意可得(-a,a-1)?[-3,1),
,条件q:-a<x<-(1-a) 由题意可得(-a,a-1)?[-3,1),故有
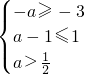 ,解得
,解得  <a≤2.
<a≤2.当-a=-(1-a)时,即a=
 ,条件q:x∈∅,显然满足p为q的一个必要不充分条件.
,条件q:x∈∅,显然满足p为q的一个必要不充分条件.综上可得,-1≤a≤2,即a的取值范围是[-1,2].
故选B.
点评:本题主要考查充分条件、必要条件、充要条件的定义和判断方法,分式不等式和一元二次不等式的解法,属于中档题

练习册系列答案
相关题目
 ;条件q:
;条件q: ,若p是q的充分不必要条件,则m的取值范围是 ( )
,若p是q的充分不必要条件,则m的取值范围是 ( )  ,条件q:
,条件q: <1,则q是
<1,则q是 p成立的( )
p成立的( ) 和条件q:
和条件q: 有意义,则
有意义,则 p是
p是