题目内容
底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的体对角线的长分别是9和15,则这个棱柱的侧面积是
160
160
.分析:根据线面垂直的定义,利用勾股定理结合题中数据算出底面菱形的对角线长分别为
和10
,再由菱形的性质算出底面的边长为8,根据直棱柱的侧面积公式加以计算,可得该棱柱的侧面积.
| 56 |
| 2 |
解答:解: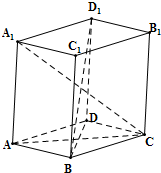 设直四棱柱ABCD-A1B1C1D1中,对角线A1C=9,BD1=15,
设直四棱柱ABCD-A1B1C1D1中,对角线A1C=9,BD1=15,
∵A1A⊥平面ABCD,AC?平面ABCD,∴A1A⊥AC,
Rt△A1AC中,A1A=5,可得AC=
=
,
同理可得BD=
=
=10
,
∵四边形ABCD为菱形,可得AC、BD互相垂直平分,
∴AB=
=
=8,即菱形ABCD的边长等于8.
因此,这个棱柱的侧面积S侧=(AB+BC+CD+DA)×A1A=4×8×5=160.
故答案为:160
 设直四棱柱ABCD-A1B1C1D1中,对角线A1C=9,BD1=15,
设直四棱柱ABCD-A1B1C1D1中,对角线A1C=9,BD1=15,∵A1A⊥平面ABCD,AC?平面ABCD,∴A1A⊥AC,
Rt△A1AC中,A1A=5,可得AC=
| A 1C2-A 1A2 |
| 56 |
同理可得BD=
| D1B2-D1D 2 |
| 200 |
| 2 |
∵四边形ABCD为菱形,可得AC、BD互相垂直平分,
∴AB=
(
|
| 14+50 |
因此,这个棱柱的侧面积S侧=(AB+BC+CD+DA)×A1A=4×8×5=160.
故答案为:160
点评:本题给出直棱柱满足的条件,求它的侧面积.着重考查了线面垂直的定义、菱形的性质和直棱柱的侧面积公式等知识,属于中档题.

练习册系列答案
相关题目