题目内容
某公司为了应对金融危机,决定适当进行裁员.已知这家公司现有职工2m人(60<m<500,且m为10的整数倍),每人每年可创利100千元.据测算,在经营条件不变的前提下,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的75%.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.问:为了获得最大的经济效益,该公司应裁员多少人?
【答案】分析:欲求获得最大的经济效益时,该公司的裁员人数.分情况求出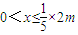 和
和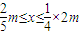 两种情况下函数的解析式,列出分段函数;分别对分段函数进行参数的讨论,最后得出裁员的最佳人数.
两种情况下函数的解析式,列出分段函数;分别对分段函数进行参数的讨论,最后得出裁员的最佳人数.
解答:解:设公司裁员人数为x,获得的经济效益为y元,
则由题意得当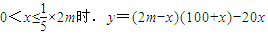 (2分)
(2分)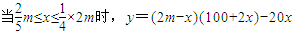 (4分)
(4分)
∴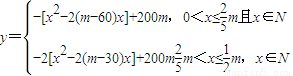 ,
,
由①得对称轴x=m-60>0,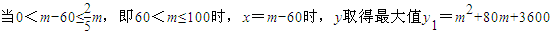
 (8分)
(8分)
由②得对称轴x=m-30,∵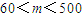 ,∴
,∴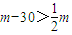 ,
,
∵
∵当60<m≤100时,y3-y1=0.5m2+60m-3600
=0.5(m+60)2-5400>0.5×1202-5400
=1800>0当100<m<500时,
y3-y2=0.86m2-12m=m(0.86m-12)>0,
即当60<m<500时,y3最大即当公司应裁员数为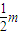 ,
,
即原有人数的 时,获得的经济效益最大. (16分)
时,获得的经济效益最大. (16分)
点评:本题考查分段函数的应用,同时考查一元二次函数最值的求法.
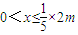 和
和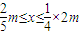 两种情况下函数的解析式,列出分段函数;分别对分段函数进行参数的讨论,最后得出裁员的最佳人数.
两种情况下函数的解析式,列出分段函数;分别对分段函数进行参数的讨论,最后得出裁员的最佳人数.解答:解:设公司裁员人数为x,获得的经济效益为y元,
则由题意得当
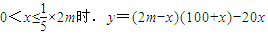 (2分)
(2分)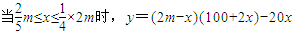 (4分)
(4分)∴
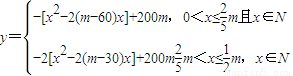 ,
,由①得对称轴x=m-60>0,
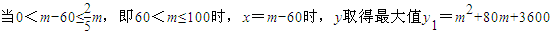
 (8分)
(8分)由②得对称轴x=m-30,∵
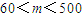 ,∴
,∴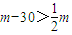 ,
,∵

∵当60<m≤100时,y3-y1=0.5m2+60m-3600
=0.5(m+60)2-5400>0.5×1202-5400
=1800>0当100<m<500时,
y3-y2=0.86m2-12m=m(0.86m-12)>0,
即当60<m<500时,y3最大即当公司应裁员数为
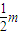 ,
,即原有人数的
 时,获得的经济效益最大. (16分)
时,获得的经济效益最大. (16分)点评:本题考查分段函数的应用,同时考查一元二次函数最值的求法.

练习册系列答案
相关题目