题目内容
已知点P (-1,| 3 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆E的方程;
(2)设A、B是椭圆E上两个动点,是否存在λ,满足
| PA |
| PB |
| PO |
| 5 |
分析:(1)由PF1⊥x轴,知F1(-1,0),c=1,F2(1,0),|PF2|=
=
,2a=|PF1|+|PF2|=4,a=2,b2=3,由此能求出椭圆E的方程.
(2)设A(x1,y1)、B(x2,y2),由
+
=λ
得(x1+1,y1-
)+(x2+1,y2-
)=λ(1,-
),所以x1+x2=λ-2,y1+y2=
(2-λ),3x12+4y12=12,3x22+4y22=12,由此得3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,AB的斜率k=
=
.设直线AB的方程为y=
x+t,与3x2+4y2=12联立消去y并整理得x2+tx+t2-3=0,再由根的判别式和点到直线AB的距离公式知这样的λ不存在.
22+(
|
| 5 |
| 2 |
(2)设A(x1,y1)、B(x2,y2),由
| PA |
| PB |
| PO |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: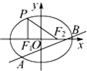 解:(1)∵PF1⊥x轴,
解:(1)∵PF1⊥x轴,
∴F1(-1,0),c=1,F2(1,0),
|PF2|=
=
,2a=|PF1|+|PF2|=4,a=2,b2=3,
椭圆E的方程为:
+
=1;(4分)
(2)设A(x1,y1)、B(x2,y2),由
+
=λ
得
(x1+1,y1-
)+(x2+1,y2-
)=λ(1,-
),
所以x1+x2=λ-2,y1+y2=
(2-λ)①(5分)
又3x12+4y12=12,3x22+4y22=12,
两式相减得3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0②
以①式代入可得AB的斜率k=
=
(8分)
设直线AB的方程为y=
x+t,
与3x2+4y2=12联立消去y并整理得x2+tx+t2-3=0,
△=3(4-t2)>0,t∈(-2,2),x1+x2=-t=λ-2
点M到直线AB的距离为d=
=
,∴t=±
∉(-2,2)(10分)
∵t=2-λ∴λ=
或-
不合题意.故这样的λ不存在(12分)
 解:(1)∵PF1⊥x轴,
解:(1)∵PF1⊥x轴,∴F1(-1,0),c=1,F2(1,0),
|PF2|=
22+(
|
| 5 |
| 2 |
椭圆E的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)设A(x1,y1)、B(x2,y2),由
| PA |
| PB |
| PO |
(x1+1,y1-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
所以x1+x2=λ-2,y1+y2=
| 3 |
| 2 |
又3x12+4y12=12,3x22+4y22=12,
两式相减得3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0②
以①式代入可得AB的斜率k=
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
设直线AB的方程为y=
| 1 |
| 2 |
与3x2+4y2=12联立消去y并整理得x2+tx+t2-3=0,
△=3(4-t2)>0,t∈(-2,2),x1+x2=-t=λ-2
点M到直线AB的距离为d=
| 2|t| | ||
|
| 5 |
| 5 |
| 2 |
∵t=2-λ∴λ=
| 9 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要灵活运用椭圆性质、点到直线距离公式、根的判别式、韦达定理,注意合理地进行等价转化.

练习册系列答案
相关题目
 已知点
已知点