题目内容
过双曲线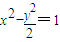 的右焦点作直线交双曲线于A,B两点,且|AB|=4,则这样的直线有 条.
的右焦点作直线交双曲线于A,B两点,且|AB|=4,则这样的直线有 条.
【答案】分析:右焦点为(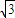 ,0),当AB的斜率不存在时,经检验满足条件,当AB的斜率存在时,设直线AB方程为y-0=k
,0),当AB的斜率不存在时,经检验满足条件,当AB的斜率存在时,设直线AB方程为y-0=k
(x-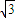 ),代入双曲线化简,求出x1+x2 和x1•x2的值,由|AB|=4=
),代入双曲线化简,求出x1+x2 和x1•x2的值,由|AB|=4=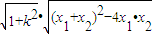 ,
,
解得k=±1,得到满足条件的斜率存在的直线有两条,故总共有3条.
解答:解:右焦点为(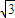 ,0),当AB的斜率不存在时,直线AB方程为 x=
,0),当AB的斜率不存在时,直线AB方程为 x= ,
,
代入双曲线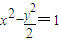 的方程可得y=±2,即A,B两点的纵坐标分别为2 和-2,满足|AB|=4.
的方程可得y=±2,即A,B两点的纵坐标分别为2 和-2,满足|AB|=4.
当AB的斜率存在时,设直线AB方程为 y-0=k(x-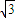 ),代入双曲线
),代入双曲线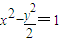 的方程化简可得
的方程化简可得
(2-k2) x2-2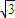 k2 x+3k2-2=0,∴x1+x2=
k2 x+3k2-2=0,∴x1+x2= ,x1•x2=
,x1•x2=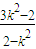 ,
,
∴|AB|=4=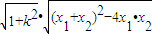 ,平方化简可得 (3k4+6)(k2-1)=0,
,平方化简可得 (3k4+6)(k2-1)=0,
∴k=±1,都能满足判别式△=12-4(2-k2)(3k2-2)>0.
所以,满足条件的且斜率存在的直线有2条.
综上,所有满足条件的直线共有3条,
故答案为 3.
点评:本题考查直线和圆锥曲线的位置关系,点到直线的距离公式,弦长公式的应用,体现了分类讨论的数学思想,求出满足条件的直线的斜率,是解题的关键和难点.
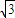 ,0),当AB的斜率不存在时,经检验满足条件,当AB的斜率存在时,设直线AB方程为y-0=k
,0),当AB的斜率不存在时,经检验满足条件,当AB的斜率存在时,设直线AB方程为y-0=k(x-
 ),代入双曲线化简,求出x1+x2 和x1•x2的值,由|AB|=4=
),代入双曲线化简,求出x1+x2 和x1•x2的值,由|AB|=4=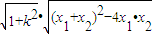 ,
,解得k=±1,得到满足条件的斜率存在的直线有两条,故总共有3条.
解答:解:右焦点为(
 ,0),当AB的斜率不存在时,直线AB方程为 x=
,0),当AB的斜率不存在时,直线AB方程为 x= ,
,代入双曲线
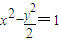 的方程可得y=±2,即A,B两点的纵坐标分别为2 和-2,满足|AB|=4.
的方程可得y=±2,即A,B两点的纵坐标分别为2 和-2,满足|AB|=4.当AB的斜率存在时,设直线AB方程为 y-0=k(x-
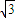 ),代入双曲线
),代入双曲线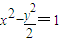 的方程化简可得
的方程化简可得(2-k2) x2-2
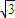 k2 x+3k2-2=0,∴x1+x2=
k2 x+3k2-2=0,∴x1+x2= ,x1•x2=
,x1•x2=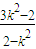 ,
,∴|AB|=4=
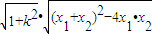 ,平方化简可得 (3k4+6)(k2-1)=0,
,平方化简可得 (3k4+6)(k2-1)=0,∴k=±1,都能满足判别式△=12-4(2-k2)(3k2-2)>0.
所以,满足条件的且斜率存在的直线有2条.
综上,所有满足条件的直线共有3条,
故答案为 3.
点评:本题考查直线和圆锥曲线的位置关系,点到直线的距离公式,弦长公式的应用,体现了分类讨论的数学思想,求出满足条件的直线的斜率,是解题的关键和难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 :
: ;则
;则 命题是;
命题是; ;
; (
( 为正整数)的展开式中,
为正整数)的展开式中, 的系数小于90,则
的系数小于90,则 .若记
.若记 ,则回归直线
,则回归直线 必过点
必过点  ;
; 的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条;
的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条; 与椭圆
与椭圆 有相同的焦点;
有相同的焦点; 、
、 为两个定点,
为两个定点, 为动点,且
为动点,且 ,其中常数
,其中常数 为正实数,则动点
为正实数,则动点 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率; 的右焦点
的右焦点 作直线
作直线 交双曲线于
交双曲线于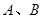 两点,若
两点,若 ,则这样的直线
,则这样的直线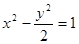 的右焦点作直线
的右焦点作直线 交双曲线于A,B两点,若|AB|=4,则满足条件的直线
交双曲线于A,B两点,若|AB|=4,则满足条件的直线