题目内容
已知F1、F2是双曲线 的两焦点,以线段F1F2为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( )
A. | B. | C. | D. |
D
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知抛物线 的焦点为
的焦点为 ,准线与
,准线与 轴的交点为
轴的交点为 ,点
,点 在
在 上且
上且 ,则
,则 的面积为( )
的面积为( )
| A.4 | B.8 | C.16 | D.32 |
抛物线 的焦点坐标是( )
的焦点坐标是( )
| A.(2,0) | B.(- 2,0) | C.(4,0) | D.(- 4,0) |
经过一定圆外一定点,并且与该圆外切的动圆圆心的轨迹是 ( )
| A.圆 | B.椭圆 | C.直线 | D.双曲线的一支 |
抛物线 上的点
上的点 到抛物线的准线的距离为
到抛物线的准线的距离为 ,到直线
,到直线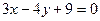 的距离为
的距离为 ,则
,则 的最小值为 ( )
的最小值为 ( )
A. | B. | C.2 | D. |
已知 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过 作椭圆的弦
作椭圆的弦 ,若
,若 的周长为16,离心率为
的周长为16,离心率为 ,则椭圆的方程为( )
,则椭圆的方程为( )
A. | B. | C. | D. |
如图,在等腰梯形 中,
中, ,且
,且 .设
.设 ,以
,以 为焦点且过点
为焦点且过点 的双曲线的离心率为
的双曲线的离心率为 ,以
,以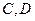 为焦点且过点
为焦点且过点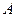 的椭圆的离心率为
的椭圆的离心率为 ,则 ( )
,则 ( )
A.随着角度 的增大, 的增大, 增大, 增大, 为定值 为定值 |
B.随着角度 的增大, 的增大, 减小, 减小, 为定值 为定值 |
C.随着角度 的增大, 的增大, 增大, 增大, 也增 也增 |
D.随着角度 的增大, 的增大, 减小, 减小, 也减小 也减小 |

椭圆 上一点
上一点 与椭圆的两个焦点
与椭圆的两个焦点 、
、 的连线互相垂直,则△
的连线互相垂直,则△ 的面积为( )
的面积为( )
A. | B. | C.24 | D.28 |
 的右顶点
的右顶点 作斜率为
作斜率为 的直线,该直线与双曲线的两条渐近线的交点分别为
的直线,该直线与双曲线的两条渐近线的交点分别为 .若
.若 ,则双曲线的离心率是 ( )
,则双曲线的离心率是 ( )


