题目内容
甲、乙两名运动员的5次测试成绩如下图所示设 分别表示甲、乙两名运动员测试成绩的标准差,
分别表示甲、乙两名运动员测试成绩的标准差,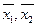 分别表示甲、乙两名运动员测试成绩的平均数,则有 ( )
分别表示甲、乙两名运动员测试成绩的平均数,则有 ( )
A. , ,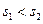 | B. , , 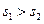 |
C.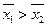 , , 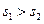 | D. , , 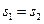 |
| 甲 | | 乙 |
| 3 5 | 1 | 4  6 6 |
| 6 6 0 | 2 | 1 4 5 |

B
解析

练习册系列答案
相关题目
某校要从高一、高二、高三共2010名学生中选取50名组成2010年上海世博会的志愿团,若采用下面的方法选取;先用简单随机抽样的方法从2010人中剔除10人,剩下的2000人再按分层抽样的方法进行,则每人入选的概率 ( )
| A.不全相等 | B.均不相等 |
C.都相等且为 | D.都相等且为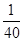 |
.甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下列联表:
| | 优秀 | 不优秀 | 合计 |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 合计 | 17 | 73 | 90 |
A.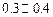 | B.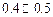 | C.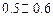 | D.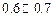 |
设有一个回归直线方程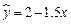 ,则变量x增加1个单位时
,则变量x增加1个单位时
| A.y平均增加1.5个单位 | B.y平均增加2个单位 |
| C.y平均减少1.5个单位 | D.y平均减少2个单位 |
甲乙丙丁四位同学各自对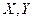 两变量的线性相关性做实验,并用回归分析方法分别求得相关系数
两变量的线性相关性做实验,并用回归分析方法分别求得相关系数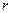 与残差平方和
与残差平方和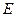 如下表:
如下表:
| | 甲 | 乙 | 丙 | 丁 |
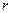 | 0.82 | 0.78 | 0.69 | 0.85 |
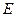 | 106 | 115 | 124 | 103 |
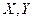 两变量具有更强的线性相关性?( )
两变量具有更强的线性相关性?( )| A.甲 | B.乙 | C.丙 | D.丁 |
为了了解我校今年准备报考飞行员的学生的体重情况,
将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1︰2︰3,第2小组的频数为12,则抽取的学生人数为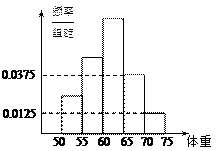
| A.46 | B.48 | C.50 | D.60 |
在研究打酣与患心脏病之间的关系中,通过收集数据、整理分析数据得“打酣与患心脏病有关”的结论,并且有 以上
以上 的把握认为这个结论是成立的。下列说法中正确的是( )
的把握认为这个结论是成立的。下列说法中正确的是( )
| A.100个心脏病患者中至少有99人打酣 | B.1个人患心脏病,则这个人有99%的概率打酣 |
| C.100个心脏病患者中一定有打酣的人 | D.100个心脏病患者中可能一个打酣的人都没有 |
在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连 续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
| A.甲地:总体均值为3,中位数为4 | B.乙地:总体均值为1,总体方差大于0 |
| C.丙地:中位数为2,众数为3 | D.丁地:总体均值为2,总体方差为3 |
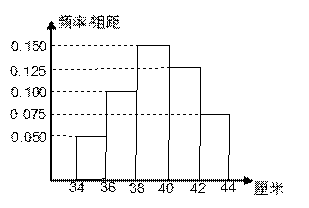
 长度的范围是[34,44],样本数据分组为[34,36),[36,38),[38,40),[40,42),[42,44]. 已知样本中产品长度小于38厘米的个数是36,则样本中净重大于或等于36厘米并且小于42厘米的产品的个数是
长度的范围是[34,44],样本数据分组为[34,36),[36,38),[38,40),[40,42),[42,44]. 已知样本中产品长度小于38厘米的个数是36,则样本中净重大于或等于36厘米并且小于42厘米的产品的个数是