题目内容
设常数a>0, 展开式中x3的系数为
展开式中x3的系数为 ,则
,则 = .
= .
【答案】分析:先利用展开式中x3的系数为 ,求出a的值,再利用无穷等比数列和的极限公式求解.
,求出a的值,再利用无穷等比数列和的极限公式求解.
解答:解:由题意,展开式的通项为
令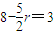 ,则r=2
,则r=2
∵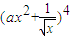 展开式中x3的系数为
展开式中x3的系数为 ,
,
∴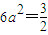
∵a>0,
∴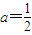
∴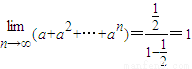
故答案为:1.
点评:本题以二项式为载体,考查数列的极限,关键是利用展开式中x3的系数为 ,求出a的值,从而求极限.
,求出a的值,从而求极限.
 ,求出a的值,再利用无穷等比数列和的极限公式求解.
,求出a的值,再利用无穷等比数列和的极限公式求解.解答:解:由题意,展开式的通项为

令
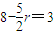 ,则r=2
,则r=2∵
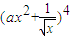 展开式中x3的系数为
展开式中x3的系数为 ,
,∴
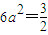
∵a>0,
∴
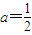
∴
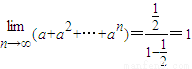
故答案为:1.
点评:本题以二项式为载体,考查数列的极限,关键是利用展开式中x3的系数为
 ,求出a的值,从而求极限.
,求出a的值,从而求极限. 
练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
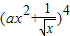 展开式中x3的系数为
展开式中x3的系数为 ,则
,则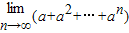 = .
= .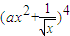 展开式中x3的系数为
展开式中x3的系数为 ,则
,则 = .
= . 展开式中x3的系数为
展开式中x3的系数为 ,则
,则 = .
= .