题目内容
在△ ABC 中,角 A、B、C 的对边分别为 a、b、c,如果  ,那么三边长a、b、c之间满足的关系是( )
,那么三边长a、b、c之间满足的关系是( )
A. B.
B. C.
C. D.
D.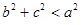
B
解析试题分析:解:在△ABC中,由cos(2B+C)+2sinAsinB<0可得,cos(B+B+C)+2sinAsinB<0.∴cosBcos(B+C)-sinBsin(B+C)+2sinAsinB<0,即 cosBcos(π-A)-sinBsin(π-A)+2sinAsinB<0.∴-cosBcosA-sinBsinA+2sinAsinB<0,-cosBcosA+sinBsinA<0.即-cos(A+B)<0,cos(A+B)>0.∴A+B<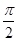 ,∴C>
,∴C>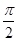 ,故△ABC形状一定是钝角三角形,故有 a2+b2<c2 .故选 B
,故△ABC形状一定是钝角三角形,故有 a2+b2<c2 .故选 B
考点:两角和与差的余弦函数公式
点评:此题考查了两角和与差的余弦函数公式,以及诱导公式,熟练掌握定理及公式是解本题的关键,属于中档题

练习册系列答案
相关题目
为得到 的图象,可将函数
的图象,可将函数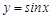 的图象向左平移
的图象向左平移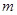 个单位长度或者向右平移
个单位长度或者向右平移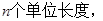
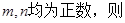
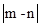 的最小值为
的最小值为
A.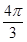 | B.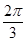 | C.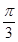 | D.2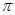 |
已知角a的终边经过点 ,则
,则 的值等于( )
的值等于( )
A. | B. | C. | D. |
若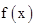 是周期为
是周期为 的奇函数,则
的奇函数,则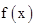 可以是( )
可以是( )
A.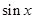 | B.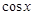 | C.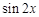 | D.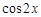 |
要得到函数 的图像,只需要将函数
的图像,只需要将函数 的图像( )
的图像( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
已知sin(θ+π)<0,cos(θ-π)>0,则下列不等关系中必定成立的是( )
| A.sinθ<0,cosθ>0 | B.sinθ>0,cosθ<0 | C.sinθ>0,cosθ>0 | D.sinθ<0,cosθ<0 |
若函数 ,又
,又 ,且
,且 的最小值为
的最小值为 ,则正数
,则正数 的值是( )
的值是( )
A. | B. | C. | D. |
若 ,且
,且 ,则下面结论正确的是( )
,则下面结论正确的是( )
A. | B. | C. | D. |
 的周期为T,在一个周期内的图像如图所示,则正确的结论是( )
的周期为T,在一个周期内的图像如图所示,则正确的结论是( )



