题目内容
f(x)= sin (ωx+φ)+cos (ωx+φ)(ω>0,|φ|<
sin (ωx+φ)+cos (ωx+φ)(ω>0,|φ|< )的最小正周期为π.且f(-x)=f(x),则下列关于g(x)=sin (ωx+φ)的图象说法正确的是( ).
)的最小正周期为π.且f(-x)=f(x),则下列关于g(x)=sin (ωx+φ)的图象说法正确的是( ).
 sin (ωx+φ)+cos (ωx+φ)(ω>0,|φ|<
sin (ωx+φ)+cos (ωx+φ)(ω>0,|φ|< )的最小正周期为π.且f(-x)=f(x),则下列关于g(x)=sin (ωx+φ)的图象说法正确的是( ).
)的最小正周期为π.且f(-x)=f(x),则下列关于g(x)=sin (ωx+φ)的图象说法正确的是( ).A.函数在x∈ 上单调递增 上单调递增 |
B.关于直线x= 对称 对称 |
C.在x∈ 上,函数值域为[0,1] 上,函数值域为[0,1] |
D.关于点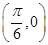 对称 对称 |
B
f(x)= sin (ωx+φ)+cos (ωx+φ)=2sin
sin (ωx+φ)+cos (ωx+φ)=2sin 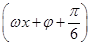 ,
,
∴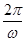 =π,即ω=2,
=π,即ω=2,
∴f(x)=2sin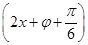 .又f(-x)=f(x),∴φ+
.又f(-x)=f(x),∴φ+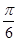 =
= ,即φ=
,即φ=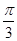 ,
,
∴g(x)=sin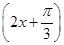 ,
,
∴当x= 时,2x+
时,2x+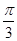 =2×
=2× +
+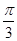 =
=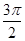 ,
,
故g(x)关于直线x= 对称.
对称.
 sin (ωx+φ)+cos (ωx+φ)=2sin
sin (ωx+φ)+cos (ωx+φ)=2sin 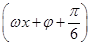 ,
,∴
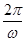 =π,即ω=2,
=π,即ω=2,∴f(x)=2sin
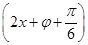 .又f(-x)=f(x),∴φ+
.又f(-x)=f(x),∴φ+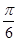 =
= ,即φ=
,即φ=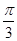 ,
,∴g(x)=sin
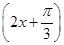 ,
,∴当x=
 时,2x+
时,2x+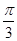 =2×
=2× +
+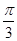 =
=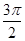 ,
,故g(x)关于直线x=
 对称.
对称.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
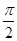 )的部分图象如图所示.
)的部分图象如图所示.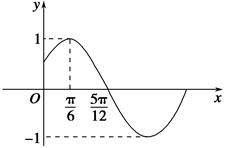
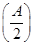 的取值范围.
的取值范围.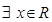 ,使
,使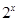 >3”的否定是“
>3”的否定是“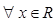 ,使
,使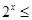 3”;
3”;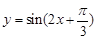 的最小正周期是
的最小正周期是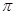 ;
;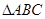 中,若
中,若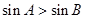 ,则
,则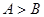 ”的逆命题是真命题;
”的逆命题是真命题;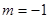 ”是“直线
”是“直线 和直线
和直线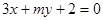 垂直”的充要
垂直”的充要 cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).
cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).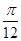



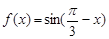 ,则要得到其导函数
,则要得到其导函数 的图象,只需将函数
的图象,只需将函数 的图象上所有的点( )
的图象上所有的点( ) 个单位长度
个单位长度  个单位长度
个单位长度 
 的最小正周期是
的最小正周期是 ,则
,则 .
. 的部分图象如图所示,为了得到g(x)=cos2x的图象,则只要将f(x)的图象( ).
的部分图象如图所示,为了得到g(x)=cos2x的图象,则只要将f(x)的图象( ).
 个单位长度
个单位长度 个单位长度
个单位长度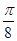 个单位长度
个单位长度 的最小正周期为 .
的最小正周期为 . )图象的对称轴方程可以为( )
)图象的对称轴方程可以为( )

