题目内容
直线l经过点P(5,5),且和圆C:x2+y2=25相交,截得弦长为![]() ,求l的方程.
,求l的方程.
答案:
解析:
提示:
解析:
|
[解法一]设直线l的方程为y-5=k(x-5)且与圆C相交于A(x1,y1)、B(x2,y2),
[规律总结]①显然解法二比解法一简单,一般地说,在解决圆和直线相交时,应首先考虑,圆心到直线的距离、弦长的一半、圆的半径构成的直角三角形,由此入手来解,可以获得简捷的解法. ②解法一虽然计算量较大,但具有一般性,适用于求一般二次曲线的弦长: |
提示:
|
若直线l的斜率不存在,l:x=5与圆C相切,可知直线l的斜率存在,设直线l的方程为y-5=k(x-5),再根据弦长|AB|= |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


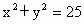 相交,截得弦长为
相交,截得弦长为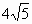 ,求l的方程.
,求l的方程.